↑

Properties

Label 2-1332-148.147-c0-0-7
Degree $2$
Conductor $1332$
Sign $-1$
Analytic cond. $0.664754$
Root an. cond. $0.815324$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − i·2-s − 4-s − 2i·5-s + i·8-s − 2·10-s + 16-s − 2i·17-s + 2i·20-s − 3·25-s + 2i·29-s − i·32-s − 2·34-s − 37-s + 2·40-s + 49-s + 3i·50-s + ⋯
L(s)  = 1  − i·2-s − 4-s − 2i·5-s + i·8-s − 2·10-s + 16-s − 2i·17-s + 2i·20-s − 3·25-s + 2i·29-s − i·32-s − 2·34-s − 37-s + 2·40-s + 49-s + 3i·50-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1332\)    =    \(2^{2} \cdot 3^{2} \cdot 37\)
Sign: $-1$
Analytic conductor: \(0.664754\)
Root analytic conductor: \(0.815324\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1332} (739, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1332,\ (\ :0),\ -1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.8518879111\)
\(L(\frac12)\) \(\approx\) \(0.8518879111\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + iT \)
3 \( 1 \)
37 \( 1 + T \)
good5 \( 1 + 2iT - T^{2} \)
7 \( 1 - T^{2} \)
11 \( 1 - T^{2} \)
13 \( 1 - T^{2} \)
17 \( 1 + 2iT - T^{2} \)
19 \( 1 + T^{2} \)
23 \( 1 + T^{2} \)
29 \( 1 - 2iT - T^{2} \)
31 \( 1 + T^{2} \)
41 \( 1 + T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 - T^{2} \)
53 \( 1 + T^{2} \)
59 \( 1 + T^{2} \)
61 \( 1 - T^{2} \)
67 \( 1 - T^{2} \)
71 \( 1 - T^{2} \)
73 \( 1 - 2T + T^{2} \)
79 \( 1 + T^{2} \)
83 \( 1 - T^{2} \)
89 \( 1 + 2iT - T^{2} \)
97 \( 1 - T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

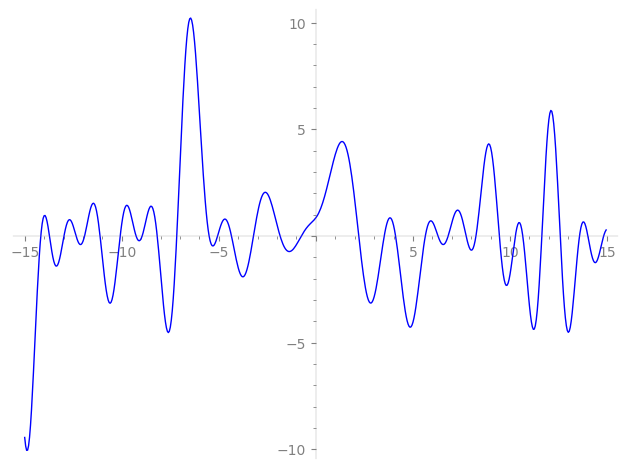
Imaginary part of the first few zeros on the critical line

−9.263316578553629191612984165716, −8.948198610174952362307836033265, −8.174508012512069959233592352296, −7.16664658589124262904547794499, −5.50116656458830640152099860584, −5.06240638219309506615955028832, −4.35031676942568073193058559590, −3.21418910234419495105039951092, −1.84593576095628764278001514242, −0.74639961767412490699413610569, 2.20670773972408657015567492181, 3.52071921081218638260797079824, 4.10210315070514634945543175068, 5.63725486358125138537236851318, 6.28692990200769658556860899977, 6.81329015461849506235384451688, 7.73669272123748992875920331166, 8.244531112739665959405529418217, 9.449464391846759011155041588538, 10.27430262381862409988665993183

Graph of the $Z$-function along the critical line