↑

Properties

Label 4-145e2-1.1-c0e2-0-1
Degree $4$
Conductor $21025$
Sign $1$
Analytic cond. $0.00523661$
Root an. cond. $0.269006$
Motivic weight $0$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

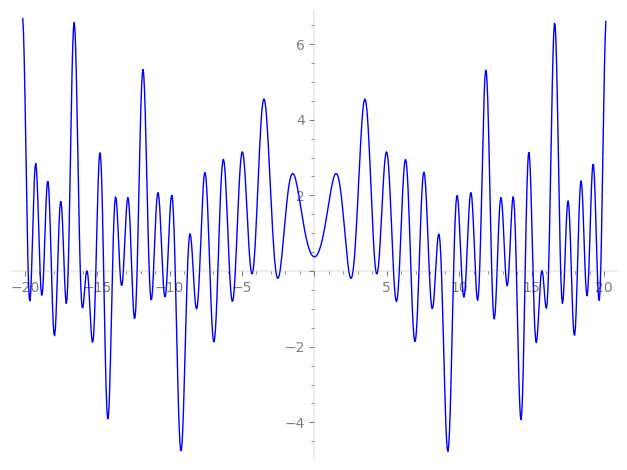
L(s)  = 1  − 2·11-s − 16-s − 2·19-s − 25-s + 2·31-s + 2·41-s + 2·49-s + 2·61-s − 2·79-s − 81-s − 2·89-s − 2·101-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s − 2·169-s + 173-s + 2·176-s + 179-s + 181-s + ⋯
L(s)  = 1  − 2·11-s − 16-s − 2·19-s − 25-s + 2·31-s + 2·41-s + 2·49-s + 2·61-s − 2·79-s − 81-s − 2·89-s − 2·101-s + 2·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s − 2·169-s + 173-s + 2·176-s + 179-s + 181-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 21025 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 21025 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(21025\)    =    \(5^{2} \cdot 29^{2}\)
Sign: $1$
Analytic conductor: \(0.00523661\)
Root analytic conductor: \(0.269006\)
Motivic weight: \(0\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 21025,\ (\ :0, 0),\ 1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.3755910542\)
\(L(\frac12)\) \(\approx\) \(0.3755910542\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad5$C_2$ \( 1 + T^{2} \)
29$C_2$ \( 1 + T^{2} \)
good2$C_2^2$ \( 1 + T^{4} \)
3$C_2^2$ \( 1 + T^{4} \)
7$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
11$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
13$C_2$ \( ( 1 + T^{2} )^{2} \)
17$C_2^2$ \( 1 + T^{4} \)
19$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
23$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
31$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
37$C_2^2$ \( 1 + T^{4} \)
41$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
43$C_2^2$ \( 1 + T^{4} \)
47$C_2^2$ \( 1 + T^{4} \)
53$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
59$C_2$ \( ( 1 + T^{2} )^{2} \)
61$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
67$C_2$ \( ( 1 + T^{2} )^{2} \)
71$C_2$ \( ( 1 + T^{2} )^{2} \)
73$C_2^2$ \( 1 + T^{4} \)
79$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
83$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
89$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
97$C_2^2$ \( 1 + T^{4} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−13.42152706905986775804239387810, −13.19007158956853907013601278393, −12.60653029703028197500961535334, −12.24017337137894231430027189121, −11.40313183987310958416432208044, −11.10773304512960009381429154755, −10.47759928528073937459323626242, −10.15441551610510815076338042987, −9.608335148010529482036674461967, −8.766585948101750623257275695389, −8.365995397532859272406981295165, −7.929057424431366116466128070148, −7.21612790594965992491197968021, −6.66425983048885149547281387292, −5.85627077927153378918702552554, −5.46047728948515655924322566353, −4.37461038896300874501784182487, −4.23963785046997912056196187044, −2.66446834598452832199469494415, −2.37441829380017958106060039538, 2.37441829380017958106060039538, 2.66446834598452832199469494415, 4.23963785046997912056196187044, 4.37461038896300874501784182487, 5.46047728948515655924322566353, 5.85627077927153378918702552554, 6.66425983048885149547281387292, 7.21612790594965992491197968021, 7.929057424431366116466128070148, 8.365995397532859272406981295165, 8.766585948101750623257275695389, 9.608335148010529482036674461967, 10.15441551610510815076338042987, 10.47759928528073937459323626242, 11.10773304512960009381429154755, 11.40313183987310958416432208044, 12.24017337137894231430027189121, 12.60653029703028197500961535334, 13.19007158956853907013601278393, 13.42152706905986775804239387810

Graph of the $Z$-function along the critical line