↑

Properties

Label 1-2e3-8.3-r1-0-0
Degree 11
Conductor 88
Sign 11
Analytic cond. 0.8597190.859719
Root an. cond. 0.8597190.859719
Motivic weight 00
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank 00

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

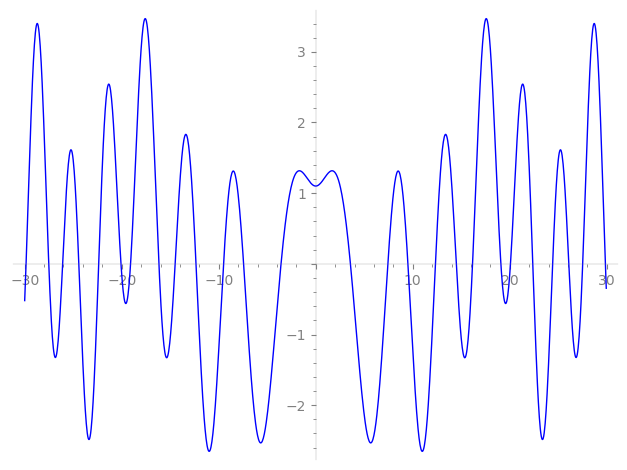
L(s)  = 1  + 3-s − 5-s − 7-s + 9-s + 11-s − 13-s − 15-s + 17-s + 19-s − 21-s − 23-s + 25-s + 27-s − 29-s − 31-s + 33-s + 35-s − 37-s − 39-s + 41-s + 43-s − 45-s − 47-s + 49-s + 51-s − 53-s − 55-s + ⋯
L(s)  = 1  + 3-s − 5-s − 7-s + 9-s + 11-s − 13-s − 15-s + 17-s + 19-s − 21-s − 23-s + 25-s + 27-s − 29-s − 31-s + 33-s + 35-s − 37-s − 39-s + 41-s + 43-s − 45-s − 47-s + 49-s + 51-s − 53-s − 55-s + ⋯

Functional equation

Λ(s)=(8s/2 ΓR(s+1) L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 8 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}
Λ(s)=(8s/2 ΓR(s+1) L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 8 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 11
Conductor: 88    =    232^{3}
Sign: 11
Analytic conductor: 0.8597190.859719
Root analytic conductor: 0.8597190.859719
Motivic weight: 00
Rational: yes
Arithmetic: yes
Character: χ8(3,⋅)\chi_{8} (3, \cdot )
Primitive: yes
Self-dual: yes
Analytic rank: 00
Selberg data: (1, 8, (1: ), 1)(1,\ 8,\ (1:\ ),\ 1)

Particular Values

L(12)L(\frac{1}{2}) ≈\approx 1.1004214091.100421409
L(12)L(\frac12) ≈\approx 1.1004214091.100421409
L(1)L(1) ≈\approx 1.1107207341.110720734
L(1)L(1) ≈\approx 1.1107207341.110720734

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
good3 1+T 1 + T
5 1−T 1 - T
7 1−T 1 - T
11 1+T 1 + T
13 1−T 1 - T
17 1+T 1 + T
19 1+T 1 + T
23 1−T 1 - T
29 1−T 1 - T
31 1−T 1 - T
37 1−T 1 - T
41 1+T 1 + T
43 1+T 1 + T
47 1−T 1 - T
53 1−T 1 - T
59 1+T 1 + T
61 1−T 1 - T
67 1+T 1 + T
71 1−T 1 - T
73 1+T 1 + T
79 1−T 1 - T
83 1+T 1 + T
89 1+T 1 + T
97 1+T 1 + T
show more
show less
   L(s)=∏p (1−αp p−s)−1L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−48.74068793215534022752522930410, −47.6209798877567549178563249871, −45.9510335880281704577596028993, −43.9346152766520649240665150339, −42.752615477159649672801727607675, −41.53981595511799883077360485981, −39.16750681241490296713715528102, −38.0617400808002403731726223796, −36.23116033995471923810665296105, −34.98256753712872018308348058124, −32.53233400657462120871686846132, −31.45201345414038079725886531059, −29.857791921026421623346922599858, −27.5181259144140394812087660182, −26.089470593190540959426835382352, −24.41964822006060936671535842043, −22.37466756829608885834718488552, −20.07363842306806925540295209504, −19.08644166006480394769355338242, −16.16469366756340984309856870967, −14.49097192816054725085740936823, −12.3405011590722115530614093056, −9.50320196197290897854598873093, −7.43447295737022101391739084615, −3.57615483678758907557757872995, 3.57615483678758907557757872995, 7.43447295737022101391739084615, 9.50320196197290897854598873093, 12.3405011590722115530614093056, 14.49097192816054725085740936823, 16.16469366756340984309856870967, 19.08644166006480394769355338242, 20.07363842306806925540295209504, 22.37466756829608885834718488552, 24.41964822006060936671535842043, 26.089470593190540959426835382352, 27.5181259144140394812087660182, 29.857791921026421623346922599858, 31.45201345414038079725886531059, 32.53233400657462120871686846132, 34.98256753712872018308348058124, 36.23116033995471923810665296105, 38.0617400808002403731726223796, 39.16750681241490296713715528102, 41.53981595511799883077360485981, 42.752615477159649672801727607675, 43.9346152766520649240665150339, 45.9510335880281704577596028993, 47.6209798877567549178563249871, 48.74068793215534022752522930410

Graph of the ZZ-function along the critical line