↑

Properties

Label 1-664-664.587-r0-0-0
Degree $1$
Conductor $664$
Sign $0.701 + 0.713i$
Analytic cond. $3.08360$
Root an. cond. $3.08360$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.817 + 0.575i)3-s + (−0.973 − 0.227i)5-s + (−0.720 − 0.693i)7-s + (0.338 + 0.941i)9-s + (−0.665 + 0.746i)11-s + (0.953 + 0.301i)13-s + (−0.665 − 0.746i)15-s + (0.606 − 0.795i)17-s + (0.543 − 0.839i)19-s + (−0.190 − 0.981i)21-s + (0.859 − 0.511i)23-s + (0.896 + 0.443i)25-s + (−0.264 + 0.964i)27-s + (0.409 + 0.912i)29-s + (−0.477 + 0.878i)31-s + ⋯
L(s)  = 1  + (0.817 + 0.575i)3-s + (−0.973 − 0.227i)5-s + (−0.720 − 0.693i)7-s + (0.338 + 0.941i)9-s + (−0.665 + 0.746i)11-s + (0.953 + 0.301i)13-s + (−0.665 − 0.746i)15-s + (0.606 − 0.795i)17-s + (0.543 − 0.839i)19-s + (−0.190 − 0.981i)21-s + (0.859 − 0.511i)23-s + (0.896 + 0.443i)25-s + (−0.264 + 0.964i)27-s + (0.409 + 0.912i)29-s + (−0.477 + 0.878i)31-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 664 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.701 + 0.713i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 664 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.701 + 0.713i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(664\)    =    \(2^{3} \cdot 83\)
Sign: $0.701 + 0.713i$
Analytic conductor: \(3.08360\)
Root analytic conductor: \(3.08360\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{664} (587, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 664,\ (0:\ ),\ 0.701 + 0.713i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.342746876 + 0.5628013016i\)
\(L(\frac12)\) \(\approx\) \(1.342746876 + 0.5628013016i\)
\(L(1)\) \(\approx\) \(1.132505642 + 0.2171023585i\)
\(L(1)\) \(\approx\) \(1.132505642 + 0.2171023585i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
83 \( 1 \)
good3 \( 1 + (0.817 + 0.575i)T \)
5 \( 1 + (-0.973 - 0.227i)T \)
7 \( 1 + (-0.720 - 0.693i)T \)
11 \( 1 + (-0.665 + 0.746i)T \)
13 \( 1 + (0.953 + 0.301i)T \)
17 \( 1 + (0.606 - 0.795i)T \)
19 \( 1 + (0.543 - 0.839i)T \)
23 \( 1 + (0.859 - 0.511i)T \)
29 \( 1 + (0.409 + 0.912i)T \)
31 \( 1 + (-0.477 + 0.878i)T \)
37 \( 1 + (-0.338 + 0.941i)T \)
41 \( 1 + (-0.771 - 0.636i)T \)
43 \( 1 + (0.264 + 0.964i)T \)
47 \( 1 + (0.988 - 0.152i)T \)
53 \( 1 + (0.988 + 0.152i)T \)
59 \( 1 + (-0.114 + 0.993i)T \)
61 \( 1 + (-0.0383 + 0.999i)T \)
67 \( 1 + (0.927 + 0.373i)T \)
71 \( 1 + (0.720 - 0.693i)T \)
73 \( 1 + (-0.896 + 0.443i)T \)
79 \( 1 + (0.190 - 0.981i)T \)
89 \( 1 + (0.997 - 0.0765i)T \)
97 \( 1 + (0.997 + 0.0765i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

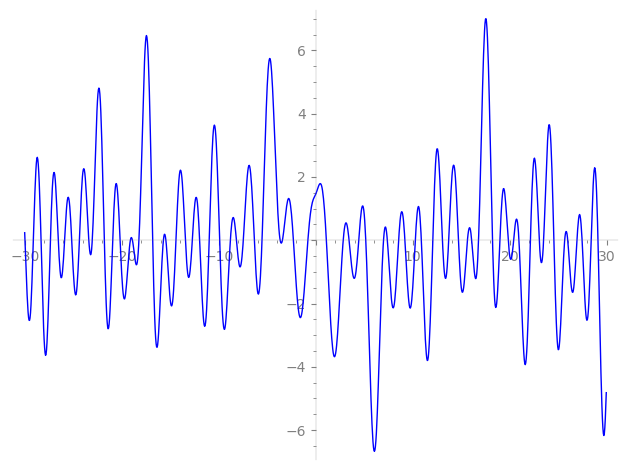
Imaginary part of the first few zeros on the critical line

−23.033388064834274304508339304206, −21.79230860976569131703288932253, −20.92995871009456466487743962804, −20.16441897666196387675525853932, −19.10714899324906352956060710067, −18.88893676184646632665985550475, −18.22379479478792657036323567189, −16.81218480680909125215183926120, −15.70255158598990499243021105794, −15.44175556009411760054496105327, −14.4066444875237693255786898294, −13.43554466899645256279685688944, −12.72317072158842486922270437421, −11.9667829519644686479807470283, −10.98326044282360331920370789860, −9.903361143427290331946044662707, −8.799036972205050480624763703177, −8.17328818561573638260030238069, −7.46618018259297158436062163321, −6.3278443345139137532404473243, −5.535740360059333413972463190, −3.66579321744007151170266617867, −3.43386976066447729319182761746, −2.30016222986481637561213688316, −0.8076899765169809588799925825, 1.09776601807613288762541739461, 2.833208217284892684282414981994, 3.43787759883869431959566656558, 4.43568163582495583407343537322, 5.15905267207824472007179062562, 6.987905197460742269989704580695, 7.382646253489651779471132383477, 8.546064719693625906753956905807, 9.193651947695783415169873551063, 10.26518453871446541976334030922, 10.88708068117042629350150515693, 12.06374120821353562408879593208, 13.061248658400515139339736741649, 13.70725753918080189953149816697, 14.71437081650746580015264731298, 15.63669658331393560816090296203, 16.07523781994191328219262054476, 16.78207256144683757483945863288, 18.22059863561722345765352664605, 18.98323440476213017336790542839, 19.83932312941541837537275073769, 20.401675368082220470462790816470, 20.94828421206284922344624807846, 22.130021343059734014109115187910, 23.04311855361144210729078119919

Graph of the $Z$-function along the critical line