↑

Properties

Label 1-703-703.322-r1-0-0
Degree $1$
Conductor $703$
Sign $0.989 - 0.146i$
Analytic cond. $75.5478$
Root an. cond. $75.5478$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.5 − 0.866i)2-s + (0.5 + 0.866i)3-s + (−0.5 − 0.866i)4-s + (−0.5 − 0.866i)5-s + 6-s + (−0.5 − 0.866i)7-s − 8-s + (−0.5 + 0.866i)9-s − 10-s + 11-s + (0.5 − 0.866i)12-s + (0.5 + 0.866i)13-s − 14-s + (0.5 − 0.866i)15-s + (−0.5 + 0.866i)16-s + (−0.5 + 0.866i)17-s + ⋯
L(s)  = 1  + (0.5 − 0.866i)2-s + (0.5 + 0.866i)3-s + (−0.5 − 0.866i)4-s + (−0.5 − 0.866i)5-s + 6-s + (−0.5 − 0.866i)7-s − 8-s + (−0.5 + 0.866i)9-s − 10-s + 11-s + (0.5 − 0.866i)12-s + (0.5 + 0.866i)13-s − 14-s + (0.5 − 0.866i)15-s + (−0.5 + 0.866i)16-s + (−0.5 + 0.866i)17-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 703 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (0.989 - 0.146i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 703 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (0.989 - 0.146i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(703\)    =    \(19 \cdot 37\)
Sign: $0.989 - 0.146i$
Analytic conductor: \(75.5478\)
Root analytic conductor: \(75.5478\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{703} (322, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 703,\ (1:\ ),\ 0.989 - 0.146i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(2.214886383 - 0.1632016681i\)
\(L(\frac12)\) \(\approx\) \(2.214886383 - 0.1632016681i\)
\(L(1)\) \(\approx\) \(1.259204728 - 0.3940463242i\)
\(L(1)\) \(\approx\) \(1.259204728 - 0.3940463242i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad19 \( 1 \)
37 \( 1 \)
good2 \( 1 + (0.5 - 0.866i)T \)
3 \( 1 + (0.5 + 0.866i)T \)
5 \( 1 + (-0.5 - 0.866i)T \)
7 \( 1 + (-0.5 - 0.866i)T \)
11 \( 1 + T \)
13 \( 1 + (0.5 + 0.866i)T \)
17 \( 1 + (-0.5 + 0.866i)T \)
23 \( 1 + T \)
29 \( 1 - T \)
31 \( 1 - T \)
41 \( 1 + (0.5 + 0.866i)T \)
43 \( 1 + T \)
47 \( 1 + T \)
53 \( 1 + (0.5 - 0.866i)T \)
59 \( 1 + (0.5 - 0.866i)T \)
61 \( 1 + (-0.5 - 0.866i)T \)
67 \( 1 + (0.5 + 0.866i)T \)
71 \( 1 + (0.5 + 0.866i)T \)
73 \( 1 + T \)
79 \( 1 + (0.5 + 0.866i)T \)
83 \( 1 + (-0.5 + 0.866i)T \)
89 \( 1 + (0.5 - 0.866i)T \)
97 \( 1 - T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

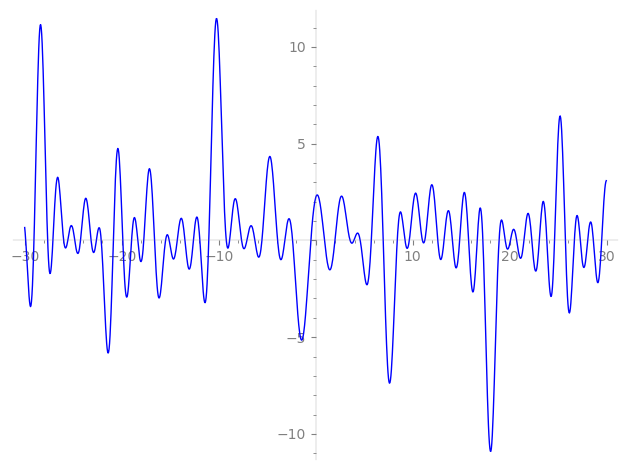
Imaginary part of the first few zeros on the critical line

−22.61049227841956367820708203093, −22.10874869746563130087303465812, −20.860996556928325740139598539979, −19.886622786815281045619134554238, −18.98672458070246060816261835542, −18.34193158655769974813297647461, −17.72514354889784778725501657846, −16.61730173146363532798549123137, −15.48089753368192091367867968675, −15.09951565992742425291175371615, −14.27595093089527776679044865011, −13.47776715005363374570717701767, −12.610659658001657245116704904539, −11.94071132845257801324873851566, −11.02390967598203215481627309868, −9.219460998242197856351722461296, −8.87791673070178492339038002074, −7.64557222229898321439398678617, −7.09730778703760841653938830852, −6.26996798101649429903055345212, −5.546059699636624839135843341143, −3.92921607927366257554929795183, −3.1879410952263701131096831092, −2.38295305887428668072140634465, −0.50418281436276016260235677445, 0.90566247410159515378412287751, 1.98257334613412273442782024232, 3.54386114478448621132613669084, 3.93317647871461973967655656542, 4.587231001543304192843002877990, 5.730169301424559512842994494126, 6.95650565150755365860194411645, 8.401082546505326943239213136110, 9.2045190274157466961860281538, 9.64526612920535223488142008854, 10.99884815577992319106323148854, 11.23909172416687176840950211083, 12.58043103680751352320892645497, 13.22658447068052320108026061613, 14.091887490664949338259732275651, 14.83595532908426994018301282205, 15.75759519568350383096456625519, 16.64779795215088020764353064102, 17.2310792150063373671219116651, 18.89730400361114864458022748153, 19.53201725337332961534988402214, 20.06840170083916296862869961721, 20.71478213494739708449041452423, 21.46367386155523473085096530480, 22.277037535822263267067001302614

Graph of the $Z$-function along the critical line