↑

Properties

Label 2-1008-48.35-c1-0-11
Degree 22
Conductor 10081008
Sign −0.484−0.874i-0.484 - 0.874i
Analytic cond. 8.048928.04892
Root an. cond. 2.837062.83706
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.11 + 0.866i)2-s + (0.496 − 1.93i)4-s + (0.925 + 0.925i)5-s + 7-s + (1.12 + 2.59i)8-s + (−1.83 − 0.231i)10-s + (−1.72 + 1.72i)11-s + (0.328 + 0.328i)13-s + (−1.11 + 0.866i)14-s + (−3.50 − 1.92i)16-s + 2.34i·17-s + (−1.77 + 1.77i)19-s + (2.25 − 1.33i)20-s + (0.431 − 3.42i)22-s + 6.17i·23-s + ⋯
L(s)  = 1  + (−0.790 + 0.613i)2-s + (0.248 − 0.968i)4-s + (0.413 + 0.413i)5-s + 0.377·7-s + (0.397 + 0.917i)8-s + (−0.580 − 0.0732i)10-s + (−0.519 + 0.519i)11-s + (0.0910 + 0.0910i)13-s + (−0.298 + 0.231i)14-s + (−0.876 − 0.481i)16-s + 0.567i·17-s + (−0.408 + 0.408i)19-s + (0.503 − 0.298i)20-s + (0.0920 − 0.729i)22-s + 1.28i·23-s + ⋯

Functional equation

Λ(s)=(1008s/2 ΓC(s) L(s)=((−0.484−0.874i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 1008 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.484 - 0.874i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(1008s/2 ΓC(s+1/2) L(s)=((−0.484−0.874i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 1008 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.484 - 0.874i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 10081008    =    24⋅32⋅72^{4} \cdot 3^{2} \cdot 7
Sign: −0.484−0.874i-0.484 - 0.874i
Analytic conductor: 8.048928.04892
Root analytic conductor: 2.837062.83706
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ1008(323,⋅)\chi_{1008} (323, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 1008, ( :1/2), −0.484−0.874i)(2,\ 1008,\ (\ :1/2),\ -0.484 - 0.874i)

Particular Values

L(1)L(1) ≈\approx 0.98132790820.9813279082
L(12)L(\frac12) ≈\approx 0.98132790820.9813279082
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(1.11−0.866i)T 1 + (1.11 - 0.866i)T
3 1 1
7 1−T 1 - T
good5 1+(−0.925−0.925i)T+5iT2 1 + (-0.925 - 0.925i)T + 5iT^{2}
11 1+(1.72−1.72i)T−11iT2 1 + (1.72 - 1.72i)T - 11iT^{2}
13 1+(−0.328−0.328i)T+13iT2 1 + (-0.328 - 0.328i)T + 13iT^{2}
17 1−2.34iT−17T2 1 - 2.34iT - 17T^{2}
19 1+(1.77−1.77i)T−19iT2 1 + (1.77 - 1.77i)T - 19iT^{2}
23 1−6.17iT−23T2 1 - 6.17iT - 23T^{2}
29 1+(0.122−0.122i)T−29iT2 1 + (0.122 - 0.122i)T - 29iT^{2}
31 1−1.74iT−31T2 1 - 1.74iT - 31T^{2}
37 1+(1.68−1.68i)T−37iT2 1 + (1.68 - 1.68i)T - 37iT^{2}
41 1−2.88T+41T2 1 - 2.88T + 41T^{2}
43 1+(−2.77−2.77i)T+43iT2 1 + (-2.77 - 2.77i)T + 43iT^{2}
47 1−5.92T+47T2 1 - 5.92T + 47T^{2}
53 1+(0.973+0.973i)T+53iT2 1 + (0.973 + 0.973i)T + 53iT^{2}
59 1+(8.33−8.33i)T−59iT2 1 + (8.33 - 8.33i)T - 59iT^{2}
61 1+(−4.28−4.28i)T+61iT2 1 + (-4.28 - 4.28i)T + 61iT^{2}
67 1+(−1.78+1.78i)T−67iT2 1 + (-1.78 + 1.78i)T - 67iT^{2}
71 1−8.57iT−71T2 1 - 8.57iT - 71T^{2}
73 1−6.41iT−73T2 1 - 6.41iT - 73T^{2}
79 1−5.38iT−79T2 1 - 5.38iT - 79T^{2}
83 1+(3.46+3.46i)T+83iT2 1 + (3.46 + 3.46i)T + 83iT^{2}
89 1+1.51T+89T2 1 + 1.51T + 89T^{2}
97 1−15.7T+97T2 1 - 15.7T + 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

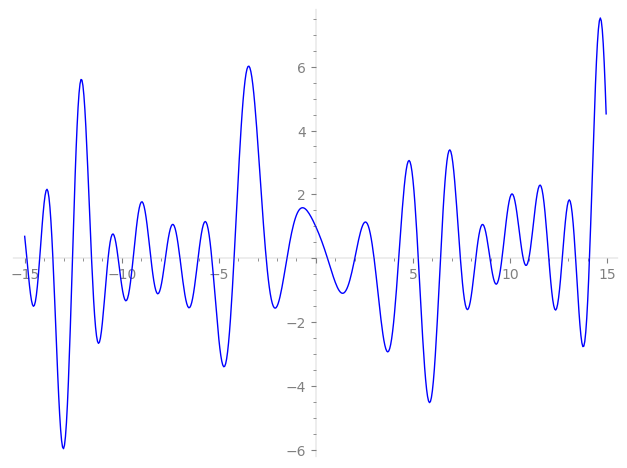
−10.18658026703153678672247825732, −9.411826990770720287004952465904, −8.500938398913285672483208772001, −7.75359700650830395804037085675, −7.00217123298436270326453993737, −6.06934810312922266953256161598, −5.36344352659258516242080191694, −4.21498837978008659273819010052, −2.56169855995675554366514275335, −1.49103427458192205789102453506, 0.59417842478559522339769354995, 2.00424101805755211644631063306, 2.99526972332116903035987840375, 4.26630720537816715604582362621, 5.27298564009275931173733443904, 6.41802054396254810763899103740, 7.44094319949178520083936129692, 8.236538911382548770283012303780, 8.964617007190674413246192911717, 9.585343294082858902506494812111

Graph of the ZZ-function along the critical line