| L(s) = 1 | − i·2-s − 4-s − i·5-s − 4.60i·7-s + i·8-s − 10-s + 3.60·13-s − 4.60·14-s + 16-s − 4.60·17-s − 4.60i·19-s + i·20-s + 1.39·23-s − 25-s − 3.60i·26-s + ⋯ |
| L(s) = 1 | − 0.707i·2-s − 0.5·4-s − 0.447i·5-s − 1.74i·7-s + 0.353i·8-s − 0.316·10-s + 1.00·13-s − 1.23·14-s + 0.250·16-s − 1.11·17-s − 1.05i·19-s + 0.223i·20-s + 0.290·23-s − 0.200·25-s − 0.707i·26-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 1170 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1170 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.170007064\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.170007064\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 + iT \) |
| 3 | \( 1 \) |
| 5 | \( 1 + iT \) |
| 13 | \( 1 - 3.60T \) |
| good | 7 | \( 1 + 4.60iT - 7T^{2} \) |
| 11 | \( 1 - 11T^{2} \) |
| 17 | \( 1 + 4.60T + 17T^{2} \) |
| 19 | \( 1 + 4.60iT - 19T^{2} \) |
| 23 | \( 1 - 1.39T + 23T^{2} \) |
| 29 | \( 1 + 4.60T + 29T^{2} \) |
| 31 | \( 1 - 6iT - 31T^{2} \) |
| 37 | \( 1 + 9.21iT - 37T^{2} \) |
| 41 | \( 1 + 3.21iT - 41T^{2} \) |
| 43 | \( 1 - 8T + 43T^{2} \) |
| 47 | \( 1 - 9.21iT - 47T^{2} \) |
| 53 | \( 1 + 6T + 53T^{2} \) |
| 59 | \( 1 - 9.21iT - 59T^{2} \) |
| 61 | \( 1 + 11.2T + 61T^{2} \) |
| 67 | \( 1 + 3.21iT - 67T^{2} \) |
| 71 | \( 1 + 9.21iT - 71T^{2} \) |
| 73 | \( 1 + 1.39iT - 73T^{2} \) |
| 79 | \( 1 + 14.4T + 79T^{2} \) |
| 83 | \( 1 + 2.78iT - 83T^{2} \) |
| 89 | \( 1 + 15.2iT - 89T^{2} \) |
| 97 | \( 1 - 1.39iT - 97T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
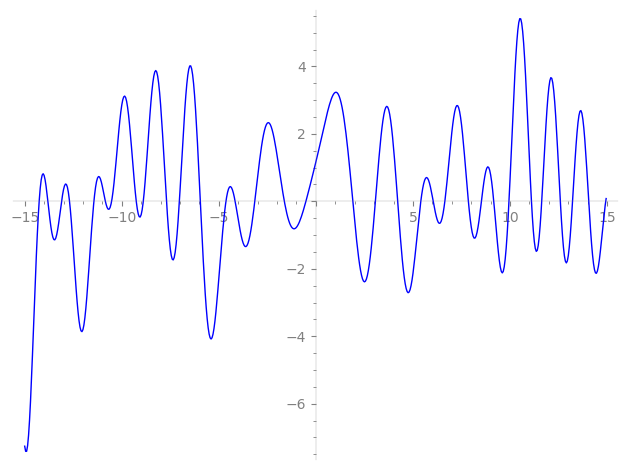
Imaginary part of the first few zeros on the critical line
−9.252645784952432429332199795045, −8.891767460786387990176091042533, −7.69396526152934103147073935464, −7.03274628397051416972650465303, −5.95308081148676960619149608294, −4.63297653432515527542396250964, −4.16042112515793033810378920628, −3.14775777238510614307352411497, −1.62545250391783214636567988570, −0.51487114833764607901905081384,
1.90099776105065766427192433005, 3.06447311149039710998548026074, 4.21200496971249717896478680118, 5.40331199792332387568937544010, 6.04304329254448087229724277265, 6.64149625038635540495788379015, 7.85416547768879583175197780591, 8.525544310527710369167190329911, 9.161138011573199076177604006441, 9.945491203669175515547786614445
