↑

Properties

Label 2-150-5.4-c3-0-5
Degree 22
Conductor 150150
Sign 0.894+0.447i0.894 + 0.447i
Analytic cond. 8.850288.85028
Root an. cond. 2.974942.97494
Motivic weight 33
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2i·2-s − 3i·3-s − 4·4-s + 6·6-s + i·7-s − 8i·8-s − 9·9-s + 42·11-s + 12i·12-s − 67i·13-s − 2·14-s + 16·16-s − 54i·17-s − 18i·18-s + 115·19-s + ⋯
L(s)  = 1  + 0.707i·2-s − 0.577i·3-s − 0.5·4-s + 0.408·6-s + 0.0539i·7-s − 0.353i·8-s − 0.333·9-s + 1.15·11-s + 0.288i·12-s − 1.42i·13-s − 0.0381·14-s + 0.250·16-s − 0.770i·17-s − 0.235i·18-s + 1.38·19-s + ⋯

Functional equation

Λ(s)=(150s/2 ΓC(s) L(s)=((0.894+0.447i) Λ‾(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 150 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.894 + 0.447i)\, \overline{\Lambda}(4-s) \end{aligned}
Λ(s)=(150s/2 ΓC(s+3/2) L(s)=((0.894+0.447i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 150 ^{s/2} \, \Gamma_{\C}(s+3/2) \, L(s)\cr =\mathstrut & (0.894 + 0.447i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 150150    =    2⋅3⋅522 \cdot 3 \cdot 5^{2}
Sign: 0.894+0.447i0.894 + 0.447i
Analytic conductor: 8.850288.85028
Root analytic conductor: 2.974942.97494
Motivic weight: 33
Rational: no
Arithmetic: yes
Character: χ150(49,⋅)\chi_{150} (49, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 150, ( :3/2), 0.894+0.447i)(2,\ 150,\ (\ :3/2),\ 0.894 + 0.447i)

Particular Values

L(2)L(2) ≈\approx 1.51767−0.358273i1.51767 - 0.358273i
L(12)L(\frac12) ≈\approx 1.51767−0.358273i1.51767 - 0.358273i
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1−2iT 1 - 2iT
3 1+3iT 1 + 3iT
5 1 1
good7 1−iT−343T2 1 - iT - 343T^{2}
11 1−42T+1.33e3T2 1 - 42T + 1.33e3T^{2}
13 1+67iT−2.19e3T2 1 + 67iT - 2.19e3T^{2}
17 1+54iT−4.91e3T2 1 + 54iT - 4.91e3T^{2}
19 1−115T+6.85e3T2 1 - 115T + 6.85e3T^{2}
23 1+162iT−1.21e4T2 1 + 162iT - 1.21e4T^{2}
29 1−210T+2.43e4T2 1 - 210T + 2.43e4T^{2}
31 1+193T+2.97e4T2 1 + 193T + 2.97e4T^{2}
37 1−286iT−5.06e4T2 1 - 286iT - 5.06e4T^{2}
41 1−12T+6.89e4T2 1 - 12T + 6.89e4T^{2}
43 1−263iT−7.95e4T2 1 - 263iT - 7.95e4T^{2}
47 1+414iT−1.03e5T2 1 + 414iT - 1.03e5T^{2}
53 1+192iT−1.48e5T2 1 + 192iT - 1.48e5T^{2}
59 1+690T+2.05e5T2 1 + 690T + 2.05e5T^{2}
61 1+733T+2.26e5T2 1 + 733T + 2.26e5T^{2}
67 1+299iT−3.00e5T2 1 + 299iT - 3.00e5T^{2}
71 1+228T+3.57e5T2 1 + 228T + 3.57e5T^{2}
73 1−938iT−3.89e5T2 1 - 938iT - 3.89e5T^{2}
79 1−160T+4.93e5T2 1 - 160T + 4.93e5T^{2}
83 1+462iT−5.71e5T2 1 + 462iT - 5.71e5T^{2}
89 1−240T+7.04e5T2 1 - 240T + 7.04e5T^{2}
97 1−511iT−9.12e5T2 1 - 511iT - 9.12e5T^{2}
show more
show less
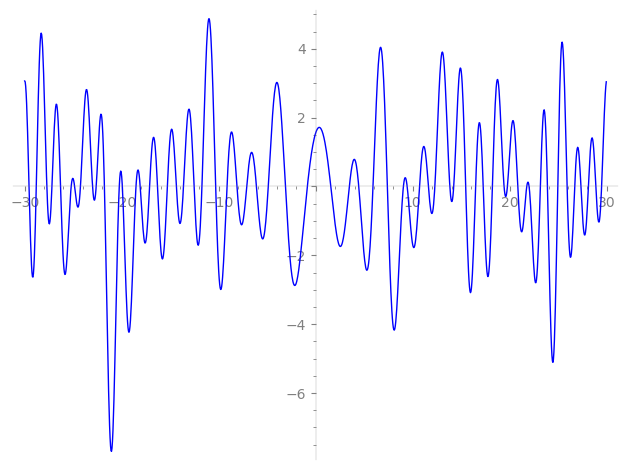
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.54057490409254281757965282229, −11.72882092462804466760756431651, −10.31581325685522804454997161309, −9.145745286441402984217522441229, −8.119807602237743918395530865958, −7.11223521662485343167009696141, −6.11117726628626872338109923775, −4.89227719407158069772713151397, −3.12373935530626252317664362402, −0.864941365152578160586413356200, 1.55349031487267319906828889420, 3.46514760153736465967703946633, 4.43486644634636739135977775392, 5.90350951884859667764036100025, 7.38139328626076788379556180652, 9.038358464480470032167562830387, 9.425627480780673480656399868532, 10.69756348222730469370161281184, 11.61708968336869741702592152970, 12.27926975492936258042810715495

Graph of the ZZ-function along the critical line