↑

Properties

Label 2-171-19.7-c3-0-6
Degree 22
Conductor 171171
Sign 0.373+0.927i0.373 + 0.927i
Analytic cond. 10.089310.0893
Root an. cond. 3.176373.17637
Motivic weight 33
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.71 − 2.97i)2-s + (−1.90 + 3.29i)4-s + (6.83 + 11.8i)5-s − 20.1·7-s − 14.4·8-s + (23.4 − 40.6i)10-s + 48.0·11-s + (34.8 − 60.3i)13-s + (34.6 + 59.9i)14-s + (39.9 + 69.2i)16-s + (58.9 + 102. i)17-s + (36.1 − 74.5i)19-s − 52.0·20-s + (−82.5 − 142. i)22-s + (35.0 − 60.7i)23-s + ⋯
L(s)  = 1  + (−0.607 − 1.05i)2-s + (−0.237 + 0.412i)4-s + (0.611 + 1.05i)5-s − 1.08·7-s − 0.636·8-s + (0.743 − 1.28i)10-s + 1.31·11-s + (0.743 − 1.28i)13-s + (0.660 + 1.14i)14-s + (0.624 + 1.08i)16-s + (0.840 + 1.45i)17-s + (0.435 − 0.899i)19-s − 0.582·20-s + (−0.799 − 1.38i)22-s + (0.317 − 0.550i)23-s + ⋯

Functional equation

Λ(s)=(171s/2 ΓC(s) L(s)=((0.373+0.927i) Λ‾(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 171 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.373 + 0.927i)\, \overline{\Lambda}(4-s) \end{aligned}
Λ(s)=(171s/2 ΓC(s+3/2) L(s)=((0.373+0.927i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 171 ^{s/2} \, \Gamma_{\C}(s+3/2) \, L(s)\cr =\mathstrut & (0.373 + 0.927i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 171171    =    32⋅193^{2} \cdot 19
Sign: 0.373+0.927i0.373 + 0.927i
Analytic conductor: 10.089310.0893
Root analytic conductor: 3.176373.17637
Motivic weight: 33
Rational: no
Arithmetic: yes
Character: χ171(64,⋅)\chi_{171} (64, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 171, ( :3/2), 0.373+0.927i)(2,\ 171,\ (\ :3/2),\ 0.373 + 0.927i)

Particular Values

L(2)L(2) ≈\approx 1.10321−0.744744i1.10321 - 0.744744i
L(12)L(\frac12) ≈\approx 1.10321−0.744744i1.10321 - 0.744744i
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1 1
19 1+(−36.1+74.5i)T 1 + (-36.1 + 74.5i)T
good2 1+(1.71+2.97i)T+(−4+6.92i)T2 1 + (1.71 + 2.97i)T + (-4 + 6.92i)T^{2}
5 1+(−6.83−11.8i)T+(−62.5+108.i)T2 1 + (-6.83 - 11.8i)T + (-62.5 + 108. i)T^{2}
7 1+20.1T+343T2 1 + 20.1T + 343T^{2}
11 1−48.0T+1.33e3T2 1 - 48.0T + 1.33e3T^{2}
13 1+(−34.8+60.3i)T+(−1.09e3−1.90e3i)T2 1 + (-34.8 + 60.3i)T + (-1.09e3 - 1.90e3i)T^{2}
17 1+(−58.9−102.i)T+(−2.45e3+4.25e3i)T2 1 + (-58.9 - 102. i)T + (-2.45e3 + 4.25e3i)T^{2}
23 1+(−35.0+60.7i)T+(−6.08e3−1.05e4i)T2 1 + (-35.0 + 60.7i)T + (-6.08e3 - 1.05e4i)T^{2}
29 1+(−102.+177.i)T+(−1.21e4−2.11e4i)T2 1 + (-102. + 177. i)T + (-1.21e4 - 2.11e4i)T^{2}
31 1−264.T+2.97e4T2 1 - 264.T + 2.97e4T^{2}
37 1+385.T+5.06e4T2 1 + 385.T + 5.06e4T^{2}
41 1+(−60.4−104.i)T+(−3.44e4+5.96e4i)T2 1 + (-60.4 - 104. i)T + (-3.44e4 + 5.96e4i)T^{2}
43 1+(−156.−270.i)T+(−3.97e4+6.88e4i)T2 1 + (-156. - 270. i)T + (-3.97e4 + 6.88e4i)T^{2}
47 1+(−57.5+99.6i)T+(−5.19e4−8.99e4i)T2 1 + (-57.5 + 99.6i)T + (-5.19e4 - 8.99e4i)T^{2}
53 1+(186.−323.i)T+(−7.44e4−1.28e5i)T2 1 + (186. - 323. i)T + (-7.44e4 - 1.28e5i)T^{2}
59 1+(−131.−228.i)T+(−1.02e5+1.77e5i)T2 1 + (-131. - 228. i)T + (-1.02e5 + 1.77e5i)T^{2}
61 1+(−143.+248.i)T+(−1.13e5−1.96e5i)T2 1 + (-143. + 248. i)T + (-1.13e5 - 1.96e5i)T^{2}
67 1+(−240.+417.i)T+(−1.50e5−2.60e5i)T2 1 + (-240. + 417. i)T + (-1.50e5 - 2.60e5i)T^{2}
71 1+(17.3+30.0i)T+(−1.78e5+3.09e5i)T2 1 + (17.3 + 30.0i)T + (-1.78e5 + 3.09e5i)T^{2}
73 1+(−352.−610.i)T+(−1.94e5+3.36e5i)T2 1 + (-352. - 610. i)T + (-1.94e5 + 3.36e5i)T^{2}
79 1+(293.+509.i)T+(−2.46e5+4.26e5i)T2 1 + (293. + 509. i)T + (-2.46e5 + 4.26e5i)T^{2}
83 1−898.T+5.71e5T2 1 - 898.T + 5.71e5T^{2}
89 1+(100.−174.i)T+(−3.52e5−6.10e5i)T2 1 + (100. - 174. i)T + (-3.52e5 - 6.10e5i)T^{2}
97 1+(7.68+13.3i)T+(−4.56e5+7.90e5i)T2 1 + (7.68 + 13.3i)T + (-4.56e5 + 7.90e5i)T^{2}
show more
show less
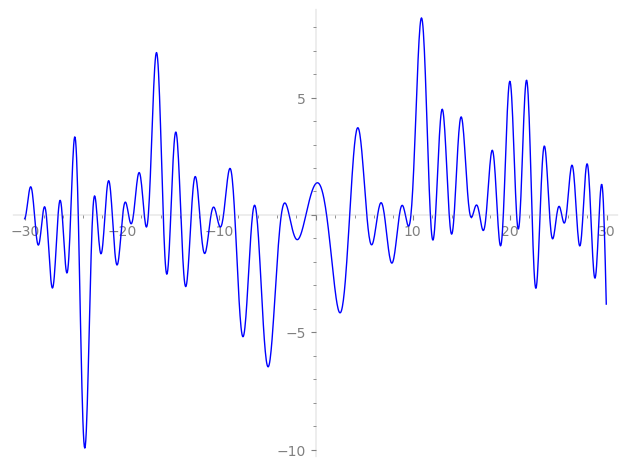
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.95352393208228645805676076116, −10.79228580432226042894047061703, −10.22467828627278844319932815107, −9.504729488071588750594562274163, −8.346412099360877292903494498130, −6.51468005086190392107881549210, −6.08868210405000905902987437159, −3.54833697203810099584164953864, −2.73974073881481828238017536947, −1.01221390170544198528583559843, 1.11955468102760875098848593742, 3.50024861080384308136876453922, 5.26526533291125369241331732629, 6.38237257503174641297967983373, 7.07573661852015800192471995367, 8.624424093846576690215913970304, 9.237913466832456475375901674610, 9.814285990183516911243412009448, 11.81785963745054157668606950066, 12.35061083036666766887120432125

Graph of the ZZ-function along the critical line