↑

Properties

Label 8-1815e4-1.1-c0e4-0-4
Degree 88
Conductor 1.085×10131.085\times 10^{13}
Sign 11
Analytic cond. 0.6731850.673185
Root an. cond. 0.9517360.951736
Motivic weight 00
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

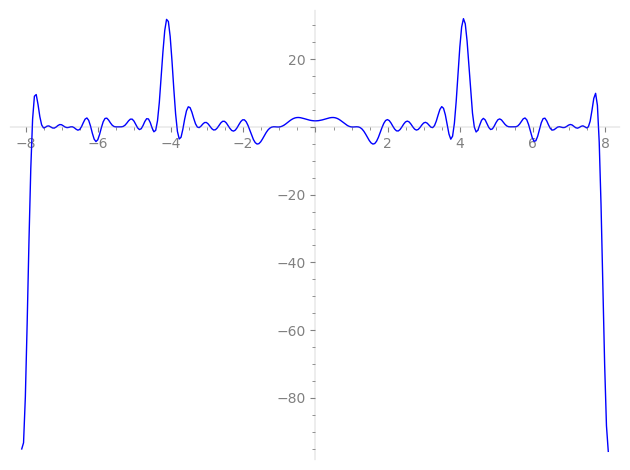
L(s)  = 1  − 3-s + 4-s + 5-s − 12-s − 15-s + 20-s + 8·23-s − 2·31-s + 2·47-s − 49-s + 2·53-s − 60-s − 8·69-s + 8·92-s + 2·93-s − 2·113-s + 8·115-s − 2·124-s + 127-s + 131-s + 137-s + 139-s − 2·141-s + 147-s + 149-s + 151-s − 2·155-s + ⋯
L(s)  = 1  − 3-s + 4-s + 5-s − 12-s − 15-s + 20-s + 8·23-s − 2·31-s + 2·47-s − 49-s + 2·53-s − 60-s − 8·69-s + 8·92-s + 2·93-s − 2·113-s + 8·115-s − 2·124-s + 127-s + 131-s + 137-s + 139-s − 2·141-s + 147-s + 149-s + 151-s − 2·155-s + ⋯

Functional equation

Λ(s)=((34⋅54⋅118)s/2 ΓC(s)4 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 5^{4} \cdot 11^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}
Λ(s)=((34⋅54⋅118)s/2 ΓC(s)4 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 5^{4} \cdot 11^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}

Invariants

Degree: 88
Conductor: 34⋅54⋅1183^{4} \cdot 5^{4} \cdot 11^{8}
Sign: 11
Analytic conductor: 0.6731850.673185
Root analytic conductor: 0.9517360.951736
Motivic weight: 00
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (8, 34⋅54⋅118, ( :0,0,0,0), 1)(8,\ 3^{4} \cdot 5^{4} \cdot 11^{8} ,\ ( \ : 0, 0, 0, 0 ),\ 1 )

Particular Values

L(12)L(\frac{1}{2}) ≈\approx 1.7629946341.762994634
L(12)L(\frac12) ≈\approx 1.7629946341.762994634
L(1)L(1) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad3C4C_4 1+T+T2+T3+T4 1 + T + T^{2} + T^{3} + T^{4}
5C4C_4 1−T+T2−T3+T4 1 - T + T^{2} - T^{3} + T^{4}
11 1 1
good2C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
7C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
13C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
17C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
19C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
23C1C_1 (1−T)8 ( 1 - T )^{8}
29C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
31C4C_4 (1+T+T2+T3+T4)2 ( 1 + T + T^{2} + T^{3} + T^{4} )^{2}
37C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
41C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
43C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
47C4C_4 (1−T+T2−T3+T4)2 ( 1 - T + T^{2} - T^{3} + T^{4} )^{2}
53C4C_4 (1−T+T2−T3+T4)2 ( 1 - T + T^{2} - T^{3} + T^{4} )^{2}
59C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
61C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
67C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
71C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
73C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
79C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
83C4×C2C_4\times C_2 1−T2+T4−T6+T8 1 - T^{2} + T^{4} - T^{6} + T^{8}
89C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
97C4C_4×\timesC4C_4 (1−T+T2−T3+T4)(1+T+T2+T3+T4) ( 1 - T + T^{2} - T^{3} + T^{4} )( 1 + T + T^{2} + T^{3} + T^{4} )
show more
show less
   L(s)=∏p ∏j=18(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−6.75976743168549194622050018298, −6.70936083732029149022481297475, −6.46240036686568621249048227451, −6.20629981546640164414514760135, −5.90537202730050813324192511362, −5.52970067268537253988029322906, −5.45847000480893646433914717494, −5.40022710397297976812335410404, −5.35899038042081557373083506983, −4.92806663331679141563735998933, −4.77869775618248663827716512182, −4.52182196098430655038893368790, −4.38750063675609260562580982950, −3.82768895340007164308622845790, −3.64951055694796944916546225112, −3.26711293045039118533479787536, −3.17829273602596063121315119260, −2.90248422150130880180294765483, −2.68851887938753586690287345124, −2.38992379716021432069759903252, −2.14810978352900364288800599568, −1.84673757713900894070225206380, −1.16989773128452195689913651419, −1.10845664957994227174785695838, −0.975605875279988683946736662856, 0.975605875279988683946736662856, 1.10845664957994227174785695838, 1.16989773128452195689913651419, 1.84673757713900894070225206380, 2.14810978352900364288800599568, 2.38992379716021432069759903252, 2.68851887938753586690287345124, 2.90248422150130880180294765483, 3.17829273602596063121315119260, 3.26711293045039118533479787536, 3.64951055694796944916546225112, 3.82768895340007164308622845790, 4.38750063675609260562580982950, 4.52182196098430655038893368790, 4.77869775618248663827716512182, 4.92806663331679141563735998933, 5.35899038042081557373083506983, 5.40022710397297976812335410404, 5.45847000480893646433914717494, 5.52970067268537253988029322906, 5.90537202730050813324192511362, 6.20629981546640164414514760135, 6.46240036686568621249048227451, 6.70936083732029149022481297475, 6.75976743168549194622050018298

Graph of the ZZ-function along the critical line