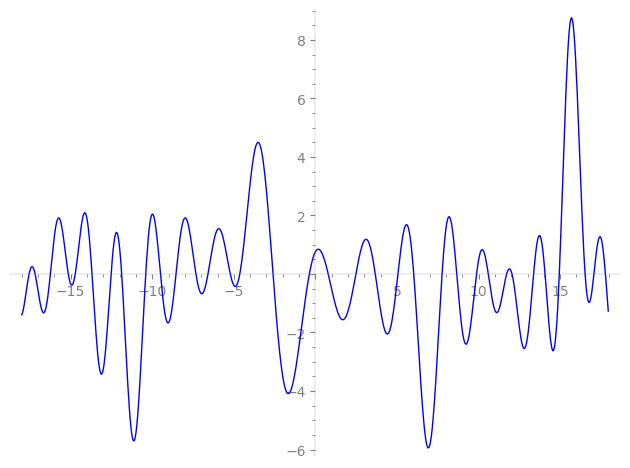
| L(s) = 1 | + (−0.375 + 5.64i)2-s − 6.67·3-s + (−31.7 − 4.24i)4-s + (2.50 − 37.6i)6-s + 38.2i·7-s + (35.8 − 177. i)8-s − 198.·9-s + 491. i·11-s + (211. + 28.3i)12-s − 956.·13-s + (−216. − 14.3i)14-s + (988. + 269. i)16-s − 339. i·17-s + (74.5 − 1.12e3i)18-s − 1.86e3i·19-s + ⋯ |
| L(s) = 1 | + (−0.0664 + 0.997i)2-s − 0.428·3-s + (−0.991 − 0.132i)4-s + (0.0284 − 0.427i)6-s + 0.295i·7-s + (0.198 − 0.980i)8-s − 0.816·9-s + 1.22i·11-s + (0.424 + 0.0567i)12-s − 1.56·13-s + (−0.294 − 0.0196i)14-s + (0.964 + 0.262i)16-s − 0.285i·17-s + (0.0542 − 0.814i)18-s − 1.18i·19-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 200 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.965 - 0.261i)\, \overline{\Lambda}(6-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 200 ^{s/2} \, \Gamma_{\C}(s+5/2) \, L(s)\cr =\mathstrut & (0.965 - 0.261i)\, \overline{\Lambda}(1-s) \end{aligned}\]
Particular Values
| \(L(3)\) |
\(\approx\) |
\(0.7591383730\) |
| \(L(\frac12)\) |
\(\approx\) |
\(0.7591383730\) |
| \(L(\frac{7}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 + (0.375 - 5.64i)T \) |
| 5 | \( 1 \) |
| good | 3 | \( 1 + 6.67T + 243T^{2} \) |
| 7 | \( 1 - 38.2iT - 1.68e4T^{2} \) |
| 11 | \( 1 - 491. iT - 1.61e5T^{2} \) |
| 13 | \( 1 + 956.T + 3.71e5T^{2} \) |
| 17 | \( 1 + 339. iT - 1.41e6T^{2} \) |
| 19 | \( 1 + 1.86e3iT - 2.47e6T^{2} \) |
| 23 | \( 1 + 1.99e3iT - 6.43e6T^{2} \) |
| 29 | \( 1 - 3.57e3iT - 2.05e7T^{2} \) |
| 31 | \( 1 - 7.71e3T + 2.86e7T^{2} \) |
| 37 | \( 1 + 2.83e3T + 6.93e7T^{2} \) |
| 41 | \( 1 - 1.06e4T + 1.15e8T^{2} \) |
| 43 | \( 1 + 2.05e4T + 1.47e8T^{2} \) |
| 47 | \( 1 - 756. iT - 2.29e8T^{2} \) |
| 53 | \( 1 - 3.16e4T + 4.18e8T^{2} \) |
| 59 | \( 1 - 4.91e3iT - 7.14e8T^{2} \) |
| 61 | \( 1 + 2.14e4iT - 8.44e8T^{2} \) |
| 67 | \( 1 - 6.81e3T + 1.35e9T^{2} \) |
| 71 | \( 1 + 1.11e4T + 1.80e9T^{2} \) |
| 73 | \( 1 - 7.30e3iT - 2.07e9T^{2} \) |
| 79 | \( 1 - 2.35e4T + 3.07e9T^{2} \) |
| 83 | \( 1 - 2.37e4T + 3.93e9T^{2} \) |
| 89 | \( 1 - 1.25e5T + 5.58e9T^{2} \) |
| 97 | \( 1 + 1.26e5iT - 8.58e9T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−11.87415535647846747253727649367, −10.39865433192023626712907947567, −9.496023013761084664166526700972, −8.544193261175441980609889723112, −7.32156328774341323869785147008, −6.58429690226209908800585505431, −5.21650345702515544607824763872, −4.63442241584018000054133859795, −2.59779569765968550260995714071, −0.37183059294762901705913955112,
0.78445078425356259116948085501, 2.48224354329757778392844375436, 3.67012567046756779811012318896, 5.05992529777862055400929135655, 6.02766796261097661736438691968, 7.76408294899487113054827498475, 8.665127014216867801376370476799, 9.875601006756145272903865277943, 10.59580864176228426389987983193, 11.72241866606345609770693659914
