↑

Properties

Label 4-2106e2-1.1-c1e2-0-35
Degree 44
Conductor 44352364435236
Sign 11
Analytic cond. 282.794282.794
Root an. cond. 4.100794.10079
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 22

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 2·2-s + 3·4-s + 2·5-s + 2·7-s − 4·8-s − 4·10-s − 8·11-s − 2·13-s − 4·14-s + 5·16-s + 6·20-s + 16·22-s + 2·23-s − 4·25-s + 4·26-s + 6·28-s − 16·29-s + 8·31-s − 6·32-s + 4·35-s − 12·37-s − 8·40-s − 6·41-s − 4·43-s − 24·44-s − 4·46-s − 8·47-s + ⋯
L(s)  = 1  − 1.41·2-s + 3/2·4-s + 0.894·5-s + 0.755·7-s − 1.41·8-s − 1.26·10-s − 2.41·11-s − 0.554·13-s − 1.06·14-s + 5/4·16-s + 1.34·20-s + 3.41·22-s + 0.417·23-s − 4/5·25-s + 0.784·26-s + 1.13·28-s − 2.97·29-s + 1.43·31-s − 1.06·32-s + 0.676·35-s − 1.97·37-s − 1.26·40-s − 0.937·41-s − 0.609·43-s − 3.61·44-s − 0.589·46-s − 1.16·47-s + ⋯

Functional equation

Λ(s)=(4435236s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 4435236 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(4435236s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 4435236 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 44352364435236    =    22⋅38⋅1322^{2} \cdot 3^{8} \cdot 13^{2}
Sign: 11
Analytic conductor: 282.794282.794
Root analytic conductor: 4.100794.10079
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 22
Selberg data: (4, 4435236, ( :1/2,1/2), 1)(4,\ 4435236,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) == 00
L(12)L(\frac12) == 00
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2C1C_1 (1+T)2 ( 1 + T )^{2}
3 1 1
13C1C_1 (1+T)2 ( 1 + T )^{2}
good5D4D_{4} 1−2T+8T2−2pT3+p2T4 1 - 2 T + 8 T^{2} - 2 p T^{3} + p^{2} T^{4}
7D4D_{4} 1−2T+3T2−2pT3+p2T4 1 - 2 T + 3 T^{2} - 2 p T^{3} + p^{2} T^{4}
11D4D_{4} 1+8T+35T2+8pT3+p2T4 1 + 8 T + 35 T^{2} + 8 p T^{3} + p^{2} T^{4}
17C22C_2^2 1−14T2+p2T4 1 - 14 T^{2} + p^{2} T^{4}
19C22C_2^2 1+35T2+p2T4 1 + 35 T^{2} + p^{2} T^{4}
23D4D_{4} 1−2T+20T2−2pT3+p2T4 1 - 2 T + 20 T^{2} - 2 p T^{3} + p^{2} T^{4}
29D4D_{4} 1+16T+119T2+16pT3+p2T4 1 + 16 T + 119 T^{2} + 16 p T^{3} + p^{2} T^{4}
31D4D_{4} 1−8T+66T2−8pT3+p2T4 1 - 8 T + 66 T^{2} - 8 p T^{3} + p^{2} T^{4}
37D4D_{4} 1+12T+98T2+12pT3+p2T4 1 + 12 T + 98 T^{2} + 12 p T^{3} + p^{2} T^{4}
41D4D_{4} 1+6T+88T2+6pT3+p2T4 1 + 6 T + 88 T^{2} + 6 p T^{3} + p^{2} T^{4}
43D4D_{4} 1+4T+42T2+4pT3+p2T4 1 + 4 T + 42 T^{2} + 4 p T^{3} + p^{2} T^{4}
47D4D_{4} 1+8T+98T2+8pT3+p2T4 1 + 8 T + 98 T^{2} + 8 p T^{3} + p^{2} T^{4}
53C22C_2^2 1+31T2+p2T4 1 + 31 T^{2} + p^{2} T^{4}
59D4D_{4} 1+4T−25T2+4pT3+p2T4 1 + 4 T - 25 T^{2} + 4 p T^{3} + p^{2} T^{4}
61D4D_{4} 1+4T+99T2+4pT3+p2T4 1 + 4 T + 99 T^{2} + 4 p T^{3} + p^{2} T^{4}
67D4D_{4} 1+4T+30T2+4pT3+p2T4 1 + 4 T + 30 T^{2} + 4 p T^{3} + p^{2} T^{4}
71D4D_{4} 1+14T+179T2+14pT3+p2T4 1 + 14 T + 179 T^{2} + 14 p T^{3} + p^{2} T^{4}
73D4D_{4} 1+20T+234T2+20pT3+p2T4 1 + 20 T + 234 T^{2} + 20 p T^{3} + p^{2} T^{4}
79D4D_{4} 1−22T+252T2−22pT3+p2T4 1 - 22 T + 252 T^{2} - 22 p T^{3} + p^{2} T^{4}
83D4D_{4} 1+12T+127T2+12pT3+p2T4 1 + 12 T + 127 T^{2} + 12 p T^{3} + p^{2} T^{4}
89D4D_{4} 1−18T+232T2−18pT3+p2T4 1 - 18 T + 232 T^{2} - 18 p T^{3} + p^{2} T^{4}
97D4D_{4} 1−22T+312T2−22pT3+p2T4 1 - 22 T + 312 T^{2} - 22 p T^{3} + p^{2} T^{4}
show more
show less
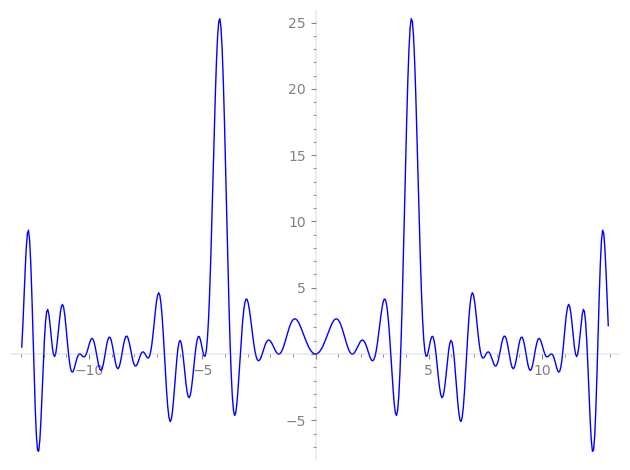
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−8.907087079188679987349114491578, −8.551114141832779612209200415234, −8.128566454951051357982948207637, −7.71176653963758680456671370099, −7.52762529710846723322839369210, −7.30175441238869628610376847070, −6.67390066077669515326965706375, −6.10442559899069989064364781896, −5.85847139206074798344123280612, −5.31840368647455923100676110416, −4.95256159029416531923328418827, −4.84688452923613685087150192246, −3.75744449828790083603113475907, −3.32195737050018164203386438444, −2.65052789659500072464411331977, −2.35737155687156421438091072128, −1.65009900268749605715328001033, −1.59742641325301888831450611010, 0, 0, 1.59742641325301888831450611010, 1.65009900268749605715328001033, 2.35737155687156421438091072128, 2.65052789659500072464411331977, 3.32195737050018164203386438444, 3.75744449828790083603113475907, 4.84688452923613685087150192246, 4.95256159029416531923328418827, 5.31840368647455923100676110416, 5.85847139206074798344123280612, 6.10442559899069989064364781896, 6.67390066077669515326965706375, 7.30175441238869628610376847070, 7.52762529710846723322839369210, 7.71176653963758680456671370099, 8.128566454951051357982948207637, 8.551114141832779612209200415234, 8.907087079188679987349114491578

Graph of the ZZ-function along the critical line