↑

Properties

Label 2-260-260.43-c1-0-25
Degree 22
Conductor 260260
Sign 0.990+0.141i0.990 + 0.141i
Analytic cond. 2.076112.07611
Root an. cond. 1.440871.44087
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.36 − 0.366i)2-s + (1.73 − i)4-s + (−0.133 + 2.23i)5-s + (1.99 − 2i)8-s + (2.59 − 1.5i)9-s + (0.633 + 3.09i)10-s + (−3.23 + 1.59i)13-s + (1.99 − 3.46i)16-s + (−0.133 − 0.0358i)17-s + (3 − 3i)18-s + (2 + 3.99i)20-s + (−4.96 − 0.598i)25-s + (−3.83 + 3.36i)26-s + (−9.23 − 5.33i)29-s + (1.46 − 5.46i)32-s + ⋯
L(s)  = 1  + (0.965 − 0.258i)2-s + (0.866 − 0.5i)4-s + (−0.0599 + 0.998i)5-s + (0.707 − 0.707i)8-s + (0.866 − 0.5i)9-s + (0.200 + 0.979i)10-s + (−0.896 + 0.443i)13-s + (0.499 − 0.866i)16-s + (−0.0324 − 0.00870i)17-s + (0.707 − 0.707i)18-s + (0.447 + 0.894i)20-s + (−0.992 − 0.119i)25-s + (−0.751 + 0.660i)26-s + (−1.71 − 0.989i)29-s + (0.258 − 0.965i)32-s + ⋯

Functional equation

Λ(s)=(260s/2 ΓC(s) L(s)=((0.990+0.141i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 260 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.990 + 0.141i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(260s/2 ΓC(s+1/2) L(s)=((0.990+0.141i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 260 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.990 + 0.141i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 260260    =    22⋅5⋅132^{2} \cdot 5 \cdot 13
Sign: 0.990+0.141i0.990 + 0.141i
Analytic conductor: 2.076112.07611
Root analytic conductor: 1.440871.44087
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ260(43,⋅)\chi_{260} (43, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 260, ( :1/2), 0.990+0.141i)(2,\ 260,\ (\ :1/2),\ 0.990 + 0.141i)

Particular Values

L(1)L(1) ≈\approx 2.19611−0.155642i2.19611 - 0.155642i
L(12)L(\frac12) ≈\approx 2.19611−0.155642i2.19611 - 0.155642i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−1.36+0.366i)T 1 + (-1.36 + 0.366i)T
5 1+(0.133−2.23i)T 1 + (0.133 - 2.23i)T
13 1+(3.23−1.59i)T 1 + (3.23 - 1.59i)T
good3 1+(−2.59+1.5i)T2 1 + (-2.59 + 1.5i)T^{2}
7 1+(6.06+3.5i)T2 1 + (6.06 + 3.5i)T^{2}
11 1+(−5.5−9.52i)T2 1 + (-5.5 - 9.52i)T^{2}
17 1+(0.133+0.0358i)T+(14.7+8.5i)T2 1 + (0.133 + 0.0358i)T + (14.7 + 8.5i)T^{2}
19 1+(9.5−16.4i)T2 1 + (9.5 - 16.4i)T^{2}
23 1+(−19.9+11.5i)T2 1 + (-19.9 + 11.5i)T^{2}
29 1+(9.23+5.33i)T+(14.5+25.1i)T2 1 + (9.23 + 5.33i)T + (14.5 + 25.1i)T^{2}
31 1+31T2 1 + 31T^{2}
37 1+(10.6−2.86i)T+(32.0−18.5i)T2 1 + (10.6 - 2.86i)T + (32.0 - 18.5i)T^{2}
41 1+(−10.3−5.96i)T+(20.5+35.5i)T2 1 + (-10.3 - 5.96i)T + (20.5 + 35.5i)T^{2}
43 1+(37.2+21.5i)T2 1 + (37.2 + 21.5i)T^{2}
47 1−47iT2 1 - 47iT^{2}
53 1+(−5.29−5.29i)T+53iT2 1 + (-5.29 - 5.29i)T + 53iT^{2}
59 1+(29.5−51.0i)T2 1 + (29.5 - 51.0i)T^{2}
61 1+(−1.33−2.30i)T+(−30.5+52.8i)T2 1 + (-1.33 - 2.30i)T + (-30.5 + 52.8i)T^{2}
67 1+(−58.0+33.5i)T2 1 + (-58.0 + 33.5i)T^{2}
71 1+(−35.5+61.4i)T2 1 + (-35.5 + 61.4i)T^{2}
73 1+(−1.16+1.16i)T−73iT2 1 + (-1.16 + 1.16i)T - 73iT^{2}
79 1+79T2 1 + 79T^{2}
83 1+83iT2 1 + 83iT^{2}
89 1+(−5+8.66i)T+(−44.5−77.0i)T2 1 + (-5 + 8.66i)T + (-44.5 - 77.0i)T^{2}
97 1+(4.75−17.7i)T+(−84.0−48.5i)T2 1 + (4.75 - 17.7i)T + (-84.0 - 48.5i)T^{2}
show more
show less
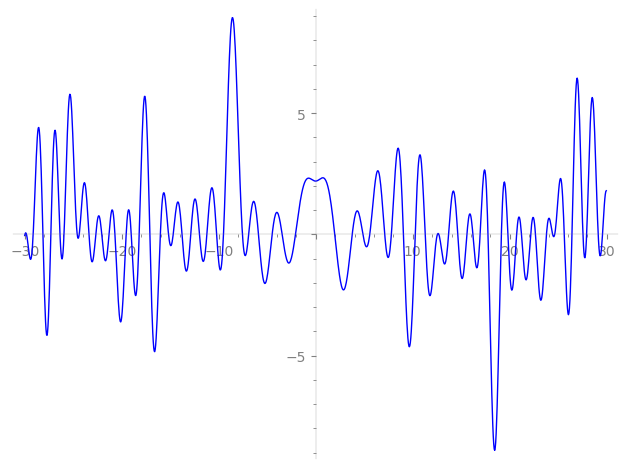
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.98021849873678474732146875670, −11.22008427892027977458233359061, −10.21471240296305693964805836261, −9.509050851451376614445355339151, −7.55302108494919958138867422268, −6.91142190369548993287531999010, −5.89933104727720344581735926307, −4.49210578042835974567409388455, −3.46000644685835524707585614927, −2.08898932961594158668462306208, 1.95942638812661455191096502919, 3.76036702768594012231891319056, 4.86561018704451972422094923930, 5.56958272668486288646026675146, 7.11521259470731472799974629183, 7.79550374872632366999366220395, 9.040700637076031427621710515298, 10.25188009445651792846460030184, 11.28209905854596109124676965112, 12.54160495714783284555854044482

Graph of the ZZ-function along the critical line