↑

Properties

Label 2-270-5.3-c2-0-12
Degree 22
Conductor 270270
Sign 0.245+0.969i0.245 + 0.969i
Analytic cond. 7.356967.35696
Root an. cond. 2.712372.71237
Motivic weight 22
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1 + i)2-s − 2i·4-s + (3.47 − 3.59i)5-s + (6.91 − 6.91i)7-s + (2 + 2i)8-s + (0.118 + 7.07i)10-s − 17.4·11-s + (−10.0 − 10.0i)13-s + 13.8i·14-s − 4·16-s + (−9.74 + 9.74i)17-s − 20.5i·19-s + (−7.18 − 6.95i)20-s + (17.4 − 17.4i)22-s + (0.673 + 0.673i)23-s + ⋯
L(s)  = 1  + (−0.5 + 0.5i)2-s − 0.5i·4-s + (0.695 − 0.718i)5-s + (0.987 − 0.987i)7-s + (0.250 + 0.250i)8-s + (0.0118 + 0.707i)10-s − 1.58·11-s + (−0.774 − 0.774i)13-s + 0.987i·14-s − 0.250·16-s + (−0.573 + 0.573i)17-s − 1.07i·19-s + (−0.359 − 0.347i)20-s + (0.792 − 0.792i)22-s + (0.0292 + 0.0292i)23-s + ⋯

Functional equation

Λ(s)=(270s/2 ΓC(s) L(s)=((0.245+0.969i) Λ‾(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 270 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.245 + 0.969i)\, \overline{\Lambda}(3-s) \end{aligned}
Λ(s)=(270s/2 ΓC(s+1) L(s)=((0.245+0.969i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 270 ^{s/2} \, \Gamma_{\C}(s+1) \, L(s)\cr =\mathstrut & (0.245 + 0.969i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 270270    =    2⋅33⋅52 \cdot 3^{3} \cdot 5
Sign: 0.245+0.969i0.245 + 0.969i
Analytic conductor: 7.356967.35696
Root analytic conductor: 2.712372.71237
Motivic weight: 22
Rational: no
Arithmetic: yes
Character: χ270(163,⋅)\chi_{270} (163, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 270, ( :1), 0.245+0.969i)(2,\ 270,\ (\ :1),\ 0.245 + 0.969i)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 0.913934−0.710978i0.913934 - 0.710978i
L(12)L(\frac12) ≈\approx 0.913934−0.710978i0.913934 - 0.710978i
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(1−i)T 1 + (1 - i)T
3 1 1
5 1+(−3.47+3.59i)T 1 + (-3.47 + 3.59i)T
good7 1+(−6.91+6.91i)T−49iT2 1 + (-6.91 + 6.91i)T - 49iT^{2}
11 1+17.4T+121T2 1 + 17.4T + 121T^{2}
13 1+(10.0+10.0i)T+169iT2 1 + (10.0 + 10.0i)T + 169iT^{2}
17 1+(9.74−9.74i)T−289iT2 1 + (9.74 - 9.74i)T - 289iT^{2}
19 1+20.5iT−361T2 1 + 20.5iT - 361T^{2}
23 1+(−0.673−0.673i)T+529iT2 1 + (-0.673 - 0.673i)T + 529iT^{2}
29 1+16.6iT−841T2 1 + 16.6iT - 841T^{2}
31 1−55.2T+961T2 1 - 55.2T + 961T^{2}
37 1+(34.9−34.9i)T−1.36e3iT2 1 + (34.9 - 34.9i)T - 1.36e3iT^{2}
41 1−54.1T+1.68e3T2 1 - 54.1T + 1.68e3T^{2}
43 1+(3.08+3.08i)T+1.84e3iT2 1 + (3.08 + 3.08i)T + 1.84e3iT^{2}
47 1+(5.65−5.65i)T−2.20e3iT2 1 + (5.65 - 5.65i)T - 2.20e3iT^{2}
53 1+(45.4+45.4i)T+2.80e3iT2 1 + (45.4 + 45.4i)T + 2.80e3iT^{2}
59 1+94.1iT−3.48e3T2 1 + 94.1iT - 3.48e3T^{2}
61 1−54.1T+3.72e3T2 1 - 54.1T + 3.72e3T^{2}
67 1+(−33.3+33.3i)T−4.48e3iT2 1 + (-33.3 + 33.3i)T - 4.48e3iT^{2}
71 1−71.8T+5.04e3T2 1 - 71.8T + 5.04e3T^{2}
73 1+(10.1+10.1i)T+5.32e3iT2 1 + (10.1 + 10.1i)T + 5.32e3iT^{2}
79 1−105.iT−6.24e3T2 1 - 105. iT - 6.24e3T^{2}
83 1+(−86.4−86.4i)T+6.88e3iT2 1 + (-86.4 - 86.4i)T + 6.88e3iT^{2}
89 1+12.4iT−7.92e3T2 1 + 12.4iT - 7.92e3T^{2}
97 1+(40.9−40.9i)T−9.40e3iT2 1 + (40.9 - 40.9i)T - 9.40e3iT^{2}
show more
show less
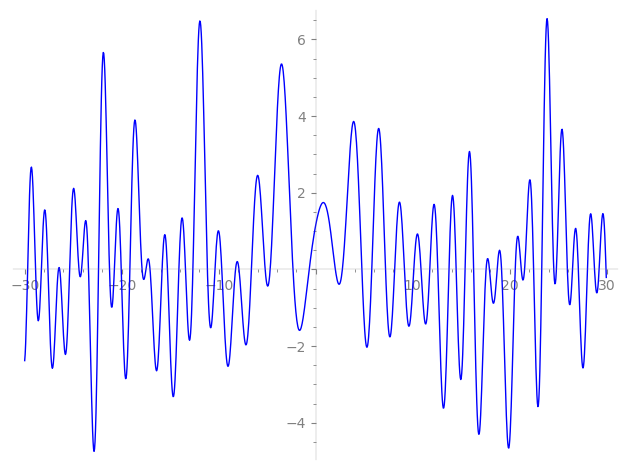
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.16910654564727674061402906936, −10.38905660546738026634482900131, −9.682596561215100468662802093073, −8.264418421227376663341561361376, −7.911543014078947000074152194644, −6.63058814484396951331323196951, −5.21163872928654980305866265414, −4.69657934892309397250991694702, −2.34437271974939728226819702891, −0.67161685326983419943729563936, 2.02281418403474007643836066484, 2.74639128598358044864235028200, 4.75543939025247428031016259734, 5.77841873597623537976064177470, 7.19573946465265657051786632460, 8.132900480789382347325073459927, 9.141672188804527126178231298312, 10.10985726684470504058584522381, 10.85548441629895627011224137279, 11.75491116225618316621920417347

Graph of the ZZ-function along the critical line