↑

Properties

Label 2-296-37.26-c1-0-6
Degree 22
Conductor 296296
Sign 0.983+0.180i0.983 + 0.180i
Analytic cond. 2.363572.36357
Root an. cond. 1.537391.53739
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.64 + 2.84i)3-s + (1.87 − 3.24i)5-s + (2.03 − 3.52i)7-s + (−3.90 − 6.77i)9-s + 1.66·11-s + (0.106 − 0.184i)13-s + (6.16 + 10.6i)15-s + (0.5 + 0.866i)17-s + (−0.271 + 0.470i)19-s + (6.69 + 11.6i)21-s − 4.61·23-s + (−4.51 − 7.82i)25-s + 15.8·27-s + 9.65·29-s − 1.66·31-s + ⋯
L(s)  = 1  + (−0.949 + 1.64i)3-s + (0.837 − 1.45i)5-s + (0.769 − 1.33i)7-s + (−1.30 − 2.25i)9-s + 0.503·11-s + (0.0295 − 0.0511i)13-s + (1.59 + 2.75i)15-s + (0.121 + 0.210i)17-s + (−0.0623 + 0.107i)19-s + (1.46 + 2.53i)21-s − 0.962·23-s + (−0.903 − 1.56i)25-s + 3.05·27-s + 1.79·29-s − 0.299·31-s + ⋯

Functional equation

Λ(s)=(296s/2 ΓC(s) L(s)=((0.983+0.180i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 296 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.983 + 0.180i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(296s/2 ΓC(s+1/2) L(s)=((0.983+0.180i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 296 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.983 + 0.180i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 296296    =    23⋅372^{3} \cdot 37
Sign: 0.983+0.180i0.983 + 0.180i
Analytic conductor: 2.363572.36357
Root analytic conductor: 1.537391.53739
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ296(137,⋅)\chi_{296} (137, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 296, ( :1/2), 0.983+0.180i)(2,\ 296,\ (\ :1/2),\ 0.983 + 0.180i)

Particular Values

L(1)L(1) ≈\approx 1.12783−0.102556i1.12783 - 0.102556i
L(12)L(\frac12) ≈\approx 1.12783−0.102556i1.12783 - 0.102556i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
37 1+(3.22−5.16i)T 1 + (3.22 - 5.16i)T
good3 1+(1.64−2.84i)T+(−1.5−2.59i)T2 1 + (1.64 - 2.84i)T + (-1.5 - 2.59i)T^{2}
5 1+(−1.87+3.24i)T+(−2.5−4.33i)T2 1 + (-1.87 + 3.24i)T + (-2.5 - 4.33i)T^{2}
7 1+(−2.03+3.52i)T+(−3.5−6.06i)T2 1 + (-2.03 + 3.52i)T + (-3.5 - 6.06i)T^{2}
11 1−1.66T+11T2 1 - 1.66T + 11T^{2}
13 1+(−0.106+0.184i)T+(−6.5−11.2i)T2 1 + (-0.106 + 0.184i)T + (-6.5 - 11.2i)T^{2}
17 1+(−0.5−0.866i)T+(−8.5+14.7i)T2 1 + (-0.5 - 0.866i)T + (-8.5 + 14.7i)T^{2}
19 1+(0.271−0.470i)T+(−9.5−16.4i)T2 1 + (0.271 - 0.470i)T + (-9.5 - 16.4i)T^{2}
23 1+4.61T+23T2 1 + 4.61T + 23T^{2}
29 1−9.65T+29T2 1 - 9.65T + 29T^{2}
31 1+1.66T+31T2 1 + 1.66T + 31T^{2}
41 1+(−0.729+1.26i)T+(−20.5−35.5i)T2 1 + (-0.729 + 1.26i)T + (-20.5 - 35.5i)T^{2}
43 1+2.74T+43T2 1 + 2.74T + 43T^{2}
47 1−3.89T+47T2 1 - 3.89T + 47T^{2}
53 1+(−3.86−6.69i)T+(−26.5+45.8i)T2 1 + (-3.86 - 6.69i)T + (-26.5 + 45.8i)T^{2}
59 1+(0.563+0.975i)T+(−29.5+51.0i)T2 1 + (0.563 + 0.975i)T + (-29.5 + 51.0i)T^{2}
61 1+(−2.85+4.95i)T+(−30.5−52.8i)T2 1 + (-2.85 + 4.95i)T + (-30.5 - 52.8i)T^{2}
67 1+(3.01−5.22i)T+(−33.5−58.0i)T2 1 + (3.01 - 5.22i)T + (-33.5 - 58.0i)T^{2}
71 1+(3.49−6.05i)T+(−35.5−61.4i)T2 1 + (3.49 - 6.05i)T + (-35.5 - 61.4i)T^{2}
73 1−2.12T+73T2 1 - 2.12T + 73T^{2}
79 1+(−4.77+8.27i)T+(−39.5−68.4i)T2 1 + (-4.77 + 8.27i)T + (-39.5 - 68.4i)T^{2}
83 1+(−6.22−10.7i)T+(−41.5+71.8i)T2 1 + (-6.22 - 10.7i)T + (-41.5 + 71.8i)T^{2}
89 1+(−2.72−4.72i)T+(−44.5+77.0i)T2 1 + (-2.72 - 4.72i)T + (-44.5 + 77.0i)T^{2}
97 1+9.99T+97T2 1 + 9.99T + 97T^{2}
show more
show less
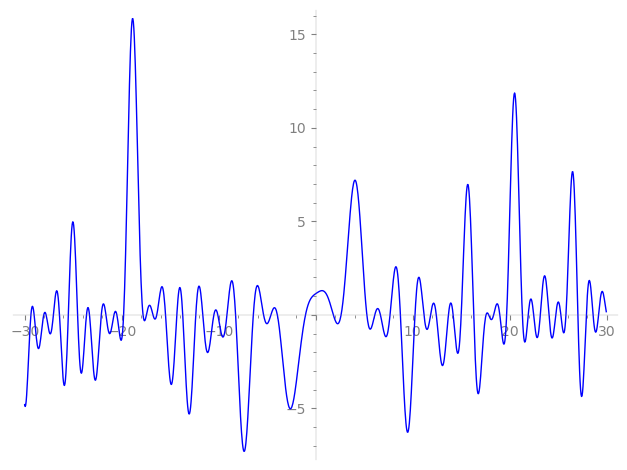
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.64289454514780989646457738394, −10.49678039833792849071029193012, −10.09427594229794734148783728481, −9.149755926111647502089947942469, −8.260014821801901100047711982238, −6.43192580154188219920422378961, −5.37618915278325509139713074930, −4.61484649399043694940939121910, −3.95755328323474478032683657618, −1.05318044361227837540908464561, 1.81586884036436769379244365660, 2.61564540665442610574924775574, 5.27138942640193230849720354291, 6.09057665585627887402551162590, 6.66764270163695705337859852451, 7.66120306060997087290318564620, 8.728779693350674513703334046595, 10.23211096865867656689422687295, 11.15555816454752241091896798644, 11.83816448979489729749279639894

Graph of the ZZ-function along the critical line