↑

Properties

Label 2-308-77.62-c1-0-5
Degree 22
Conductor 308308
Sign 0.998−0.0448i0.998 - 0.0448i
Analytic cond. 2.459392.45939
Root an. cond. 1.568241.56824
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.51 + 0.493i)3-s + (0.260 + 0.359i)5-s + (1.55 − 2.14i)7-s + (−0.366 − 0.266i)9-s + (2.44 − 2.23i)11-s + (2.91 + 2.12i)13-s + (0.218 + 0.673i)15-s + (−1.73 + 1.26i)17-s + (−2.60 + 8.03i)19-s + (3.41 − 2.48i)21-s + 1.73·23-s + (1.48 − 4.56i)25-s + (−3.23 − 4.45i)27-s + (−6.19 + 2.01i)29-s + (−2.85 + 3.92i)31-s + ⋯
L(s)  = 1  + (0.876 + 0.284i)3-s + (0.116 + 0.160i)5-s + (0.586 − 0.809i)7-s + (−0.122 − 0.0887i)9-s + (0.737 − 0.675i)11-s + (0.809 + 0.588i)13-s + (0.0565 + 0.174i)15-s + (−0.420 + 0.305i)17-s + (−0.598 + 1.84i)19-s + (0.744 − 0.542i)21-s + 0.361·23-s + (0.296 − 0.913i)25-s + (−0.623 − 0.857i)27-s + (−1.14 + 0.373i)29-s + (−0.512 + 0.704i)31-s + ⋯

Functional equation

Λ(s)=(308s/2 ΓC(s) L(s)=((0.998−0.0448i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 308 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.998 - 0.0448i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(308s/2 ΓC(s+1/2) L(s)=((0.998−0.0448i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 308 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.998 - 0.0448i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 308308    =    22⋅7⋅112^{2} \cdot 7 \cdot 11
Sign: 0.998−0.0448i0.998 - 0.0448i
Analytic conductor: 2.459392.45939
Root analytic conductor: 1.568241.56824
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ308(293,⋅)\chi_{308} (293, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 308, ( :1/2), 0.998−0.0448i)(2,\ 308,\ (\ :1/2),\ 0.998 - 0.0448i)

Particular Values

L(1)L(1) ≈\approx 1.80757+0.0405194i1.80757 + 0.0405194i
L(12)L(\frac12) ≈\approx 1.80757+0.0405194i1.80757 + 0.0405194i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
7 1+(−1.55+2.14i)T 1 + (-1.55 + 2.14i)T
11 1+(−2.44+2.23i)T 1 + (-2.44 + 2.23i)T
good3 1+(−1.51−0.493i)T+(2.42+1.76i)T2 1 + (-1.51 - 0.493i)T + (2.42 + 1.76i)T^{2}
5 1+(−0.260−0.359i)T+(−1.54+4.75i)T2 1 + (-0.260 - 0.359i)T + (-1.54 + 4.75i)T^{2}
13 1+(−2.91−2.12i)T+(4.01+12.3i)T2 1 + (-2.91 - 2.12i)T + (4.01 + 12.3i)T^{2}
17 1+(1.73−1.26i)T+(5.25−16.1i)T2 1 + (1.73 - 1.26i)T + (5.25 - 16.1i)T^{2}
19 1+(2.60−8.03i)T+(−15.3−11.1i)T2 1 + (2.60 - 8.03i)T + (-15.3 - 11.1i)T^{2}
23 1−1.73T+23T2 1 - 1.73T + 23T^{2}
29 1+(6.19−2.01i)T+(23.4−17.0i)T2 1 + (6.19 - 2.01i)T + (23.4 - 17.0i)T^{2}
31 1+(2.85−3.92i)T+(−9.57−29.4i)T2 1 + (2.85 - 3.92i)T + (-9.57 - 29.4i)T^{2}
37 1+(−0.305−0.940i)T+(−29.9+21.7i)T2 1 + (-0.305 - 0.940i)T + (-29.9 + 21.7i)T^{2}
41 1+(−2.71+8.34i)T+(−33.1−24.0i)T2 1 + (-2.71 + 8.34i)T + (-33.1 - 24.0i)T^{2}
43 1−4.32iT−43T2 1 - 4.32iT - 43T^{2}
47 1+(6.63+2.15i)T+(38.0+27.6i)T2 1 + (6.63 + 2.15i)T + (38.0 + 27.6i)T^{2}
53 1+(7.09+5.15i)T+(16.3+50.4i)T2 1 + (7.09 + 5.15i)T + (16.3 + 50.4i)T^{2}
59 1+(−10.2+3.34i)T+(47.7−34.6i)T2 1 + (-10.2 + 3.34i)T + (47.7 - 34.6i)T^{2}
61 1+(5.62−4.08i)T+(18.8−58.0i)T2 1 + (5.62 - 4.08i)T + (18.8 - 58.0i)T^{2}
67 1−11.4T+67T2 1 - 11.4T + 67T^{2}
71 1+(10.6−7.70i)T+(21.9−67.5i)T2 1 + (10.6 - 7.70i)T + (21.9 - 67.5i)T^{2}
73 1+(2.23+6.86i)T+(−59.0+42.9i)T2 1 + (2.23 + 6.86i)T + (-59.0 + 42.9i)T^{2}
79 1+(5.15−7.09i)T+(−24.4−75.1i)T2 1 + (5.15 - 7.09i)T + (-24.4 - 75.1i)T^{2}
83 1+(12.6−9.18i)T+(25.6−78.9i)T2 1 + (12.6 - 9.18i)T + (25.6 - 78.9i)T^{2}
89 1−3.04iT−89T2 1 - 3.04iT - 89T^{2}
97 1+(−0.726+0.999i)T+(−29.9−92.2i)T2 1 + (-0.726 + 0.999i)T + (-29.9 - 92.2i)T^{2}
show more
show less
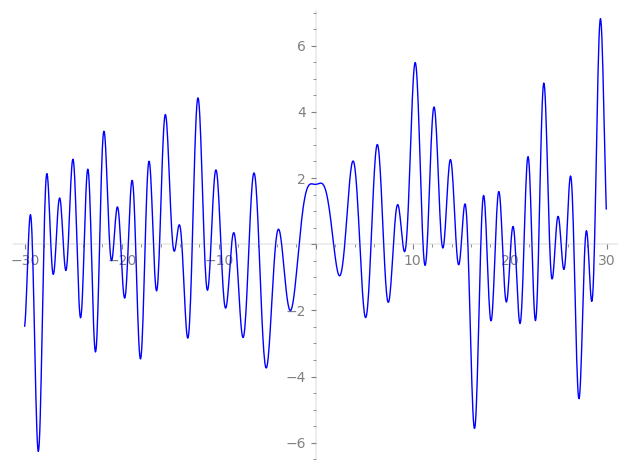
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.48946665675207452303822105067, −10.79710365219596578119037096289, −9.775094807364677980196812668849, −8.667883132698679208124747923463, −8.239592491527137936577713275462, −6.87359367440994241056191017641, −5.85614600497781662585524657917, −4.13296654115164359096352753969, −3.51595144571786382892682246850, −1.70881354820295562751692956296, 1.84394543557431530139024722311, 2.99066430975550622045664654459, 4.54872637537364151785604473613, 5.69958359721651625878759432234, 7.00643641130979328005223527821, 8.012848806444426398356952700913, 8.981123772692025053811551622293, 9.316993285190711213719986278807, 11.05952192879820019891286384545, 11.49102211392283986784796800991

Graph of the ZZ-function along the critical line