↑

Properties

Label 2-315-21.20-c9-0-72
Degree 22
Conductor 315315
Sign 0.317+0.948i0.317 + 0.948i
Analytic cond. 162.236162.236
Root an. cond. 12.737212.7372
Motivic weight 99
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 4.15i·2-s + 494.·4-s + 625·5-s + (−3.75e3 + 5.12e3i)7-s − 4.18e3i·8-s − 2.59e3i·10-s − 3.49e4i·11-s − 3.89e4i·13-s + (2.13e4 + 1.56e4i)14-s + 2.35e5·16-s + 1.12e5·17-s − 3.35e5i·19-s + 3.09e5·20-s − 1.45e5·22-s + 9.47e5i·23-s + ⋯
L(s)  = 1  − 0.183i·2-s + 0.966·4-s + 0.447·5-s + (−0.590 + 0.807i)7-s − 0.361i·8-s − 0.0821i·10-s − 0.719i·11-s − 0.378i·13-s + (0.148 + 0.108i)14-s + 0.899·16-s + 0.327·17-s − 0.590i·19-s + 0.432·20-s − 0.132·22-s + 0.706i·23-s + ⋯

Functional equation

Λ(s)=(315s/2 ΓC(s) L(s)=((0.317+0.948i) Λ‾(10−s)\begin{aligned}\Lambda(s)=\mathstrut & 315 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.317 + 0.948i)\, \overline{\Lambda}(10-s) \end{aligned}
Λ(s)=(315s/2 ΓC(s+9/2) L(s)=((0.317+0.948i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 315 ^{s/2} \, \Gamma_{\C}(s+9/2) \, L(s)\cr =\mathstrut & (0.317 + 0.948i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 315315    =    32⋅5⋅73^{2} \cdot 5 \cdot 7
Sign: 0.317+0.948i0.317 + 0.948i
Analytic conductor: 162.236162.236
Root analytic conductor: 12.737212.7372
Motivic weight: 99
Rational: no
Arithmetic: yes
Character: χ315(251,⋅)\chi_{315} (251, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 315, ( :9/2), 0.317+0.948i)(2,\ 315,\ (\ :9/2),\ 0.317 + 0.948i)

Particular Values

L(5)L(5) ≈\approx 2.7934956812.793495681
L(12)L(\frac12) ≈\approx 2.7934956812.793495681
L(112)L(\frac{11}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1 1
5 1−625T 1 - 625T
7 1+(3.75e3−5.12e3i)T 1 + (3.75e3 - 5.12e3i)T
good2 1+4.15iT−512T2 1 + 4.15iT - 512T^{2}
11 1+3.49e4iT−2.35e9T2 1 + 3.49e4iT - 2.35e9T^{2}
13 1+3.89e4iT−1.06e10T2 1 + 3.89e4iT - 1.06e10T^{2}
17 1−1.12e5T+1.18e11T2 1 - 1.12e5T + 1.18e11T^{2}
19 1+3.35e5iT−3.22e11T2 1 + 3.35e5iT - 3.22e11T^{2}
23 1−9.47e5iT−1.80e12T2 1 - 9.47e5iT - 1.80e12T^{2}
29 1−4.08e6iT−1.45e13T2 1 - 4.08e6iT - 1.45e13T^{2}
31 1+8.08e6iT−2.64e13T2 1 + 8.08e6iT - 2.64e13T^{2}
37 1+1.32e7T+1.29e14T2 1 + 1.32e7T + 1.29e14T^{2}
41 1−1.93e7T+3.27e14T2 1 - 1.93e7T + 3.27e14T^{2}
43 1−2.20e7T+5.02e14T2 1 - 2.20e7T + 5.02e14T^{2}
47 1+4.71e7T+1.11e15T2 1 + 4.71e7T + 1.11e15T^{2}
53 1+7.62e7iT−3.29e15T2 1 + 7.62e7iT - 3.29e15T^{2}
59 1−9.15e6T+8.66e15T2 1 - 9.15e6T + 8.66e15T^{2}
61 1−5.25e7iT−1.16e16T2 1 - 5.25e7iT - 1.16e16T^{2}
67 1−2.14e8T+2.72e16T2 1 - 2.14e8T + 2.72e16T^{2}
71 1+3.10e8iT−4.58e16T2 1 + 3.10e8iT - 4.58e16T^{2}
73 1+8.91e7iT−5.88e16T2 1 + 8.91e7iT - 5.88e16T^{2}
79 1−2.43e8T+1.19e17T2 1 - 2.43e8T + 1.19e17T^{2}
83 1+6.31e8T+1.86e17T2 1 + 6.31e8T + 1.86e17T^{2}
89 1+3.86e8T+3.50e17T2 1 + 3.86e8T + 3.50e17T^{2}
97 1+6.75e8iT−7.60e17T2 1 + 6.75e8iT - 7.60e17T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

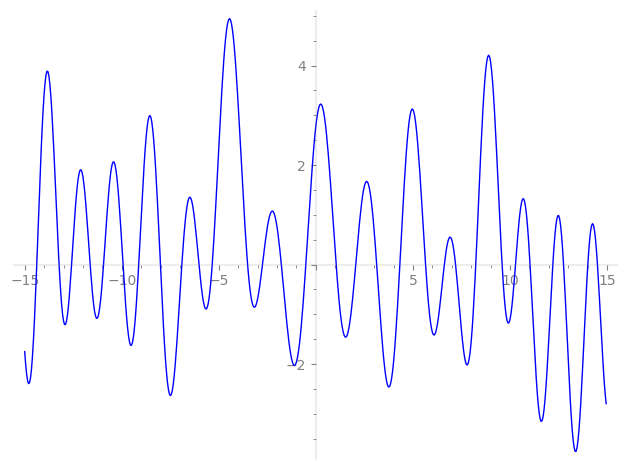
−9.934546942609440041802145673283, −9.127206176951515946973929950227, −8.009137063705110255534962134341, −6.90491214640955027259644782285, −6.02010003847087902338704991391, −5.34004968825980270739752721121, −3.51773679449601659847479075102, −2.75259043174573709576140822658, −1.78010153754980051233715086645, −0.51967392454528699313824876076, 1.04234189538211737082684581446, 2.05243052608031061835785810493, 3.13133941401914263616025632945, 4.32364821940357550038574547059, 5.64881566612348874147382216058, 6.61633197000864840738056862064, 7.19312077844128740071471714492, 8.233670672369317773393814565124, 9.590270057186501246434863367577, 10.28119405834040478700363764385

Graph of the ZZ-function along the critical line