↑

Properties

Label 2-3332-476.179-c0-0-3
Degree $2$
Conductor $3332$
Sign $0.989 + 0.142i$
Analytic cond. $1.66288$
Root an. cond. $1.28952$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

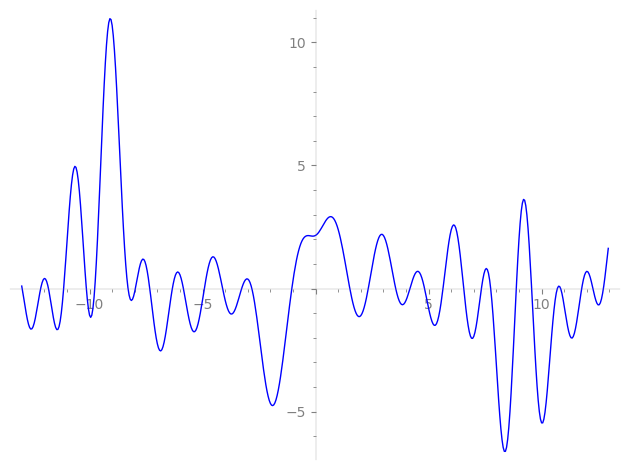
L(s)  = 1  + (0.965 + 0.258i)2-s + (0.866 + 0.499i)4-s + (−0.758 + 0.0999i)5-s + (0.707 + 0.707i)8-s + (0.258 − 0.965i)9-s + (−0.758 − 0.0999i)10-s − 2i·13-s + (0.500 + 0.866i)16-s + (0.965 − 0.258i)17-s + (0.499 − 0.866i)18-s + (−0.707 − 0.292i)20-s + (−0.400 + 0.107i)25-s + (0.517 − 1.93i)26-s + (0.707 − 1.70i)29-s + (0.258 + 0.965i)32-s + ⋯
L(s)  = 1  + (0.965 + 0.258i)2-s + (0.866 + 0.499i)4-s + (−0.758 + 0.0999i)5-s + (0.707 + 0.707i)8-s + (0.258 − 0.965i)9-s + (−0.758 − 0.0999i)10-s − 2i·13-s + (0.500 + 0.866i)16-s + (0.965 − 0.258i)17-s + (0.499 − 0.866i)18-s + (−0.707 − 0.292i)20-s + (−0.400 + 0.107i)25-s + (0.517 − 1.93i)26-s + (0.707 − 1.70i)29-s + (0.258 + 0.965i)32-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.989 + 0.142i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.989 + 0.142i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3332\)    =    \(2^{2} \cdot 7^{2} \cdot 17\)
Sign: $0.989 + 0.142i$
Analytic conductor: \(1.66288\)
Root analytic conductor: \(1.28952\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3332} (655, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3332,\ (\ :0),\ 0.989 + 0.142i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(2.159351398\)
\(L(\frac12)\) \(\approx\) \(2.159351398\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.965 - 0.258i)T \)
7 \( 1 \)
17 \( 1 + (-0.965 + 0.258i)T \)
good3 \( 1 + (-0.258 + 0.965i)T^{2} \)
5 \( 1 + (0.758 - 0.0999i)T + (0.965 - 0.258i)T^{2} \)
11 \( 1 + (0.965 + 0.258i)T^{2} \)
13 \( 1 + 2iT - T^{2} \)
19 \( 1 + (-0.866 - 0.5i)T^{2} \)
23 \( 1 + (-0.258 - 0.965i)T^{2} \)
29 \( 1 + (-0.707 + 1.70i)T + (-0.707 - 0.707i)T^{2} \)
31 \( 1 + (-0.258 + 0.965i)T^{2} \)
37 \( 1 + (-0.241 - 1.83i)T + (-0.965 + 0.258i)T^{2} \)
41 \( 1 + (-0.707 - 1.70i)T + (-0.707 + 0.707i)T^{2} \)
43 \( 1 - iT^{2} \)
47 \( 1 + (-0.5 + 0.866i)T^{2} \)
53 \( 1 + (0.366 + 1.36i)T + (-0.866 + 0.5i)T^{2} \)
59 \( 1 + (-0.866 + 0.5i)T^{2} \)
61 \( 1 + (1.12 - 1.46i)T + (-0.258 - 0.965i)T^{2} \)
67 \( 1 + (0.5 + 0.866i)T^{2} \)
71 \( 1 + (-0.707 - 0.707i)T^{2} \)
73 \( 1 + (-0.465 - 0.607i)T + (-0.258 + 0.965i)T^{2} \)
79 \( 1 + (-0.258 - 0.965i)T^{2} \)
83 \( 1 + iT^{2} \)
89 \( 1 + (0.5 - 0.866i)T^{2} \)
97 \( 1 + (-0.292 + 0.707i)T + (-0.707 - 0.707i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.296338926915897265031181400278, −7.972728831318144968301114443732, −7.33536404702883153314583440712, −6.33601972275482410971678787166, −5.84688512575265743694388643770, −4.91999534864528773051790066927, −4.11231490799299280002807728559, −3.27012524113220729940719904255, −2.81929553358394672626968431942, −1.05036628784670315363344964580, 1.51601818799201995453862550902, 2.33148123389208182931169255910, 3.54622319367956861352127656597, 4.17605824494261548442777343022, 4.82196630763423510199821965572, 5.63791718991454322497122525005, 6.55556229380696330112643496625, 7.33786990202874253531838727636, 7.74732088415036399044420867513, 8.879790457166942494605430963277

Graph of the $Z$-function along the critical line