↑

Properties

Label 2-15e3-3.2-c0-0-1
Degree $2$
Conductor $3375$
Sign $-1$
Analytic cond. $1.68434$
Root an. cond. $1.29782$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 1.33i·2-s − 0.790·4-s + 0.279i·8-s − 1.16·16-s + 1.82i·17-s − 1.33·19-s + 0.209i·23-s + 1.82·31-s − 1.27i·32-s − 2.44·34-s − 1.79i·38-s − 0.279·46-s + 0.618i·47-s − 49-s + 1.95i·53-s + ⋯
L(s)  = 1  + 1.33i·2-s − 0.790·4-s + 0.279i·8-s − 1.16·16-s + 1.82i·17-s − 1.33·19-s + 0.209i·23-s + 1.82·31-s − 1.27i·32-s − 2.44·34-s − 1.79i·38-s − 0.279·46-s + 0.618i·47-s − 49-s + 1.95i·53-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3375 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3375 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3375\)    =    \(3^{3} \cdot 5^{3}\)
Sign: $-1$
Analytic conductor: \(1.68434\)
Root analytic conductor: \(1.29782\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3375} (1376, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3375,\ (\ :0),\ -1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.049446922\)
\(L(\frac12)\) \(\approx\) \(1.049446922\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 \)
5 \( 1 \)
good2 \( 1 - 1.33iT - T^{2} \)
7 \( 1 + T^{2} \)
11 \( 1 - T^{2} \)
13 \( 1 + T^{2} \)
17 \( 1 - 1.82iT - T^{2} \)
19 \( 1 + 1.33T + T^{2} \)
23 \( 1 - 0.209iT - T^{2} \)
29 \( 1 - T^{2} \)
31 \( 1 - 1.82T + T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 - T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 - 0.618iT - T^{2} \)
53 \( 1 - 1.95iT - T^{2} \)
59 \( 1 - T^{2} \)
61 \( 1 + 1.95T + T^{2} \)
67 \( 1 + T^{2} \)
71 \( 1 - T^{2} \)
73 \( 1 + T^{2} \)
79 \( 1 - 1.95T + T^{2} \)
83 \( 1 - 1.95iT - T^{2} \)
89 \( 1 - T^{2} \)
97 \( 1 + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

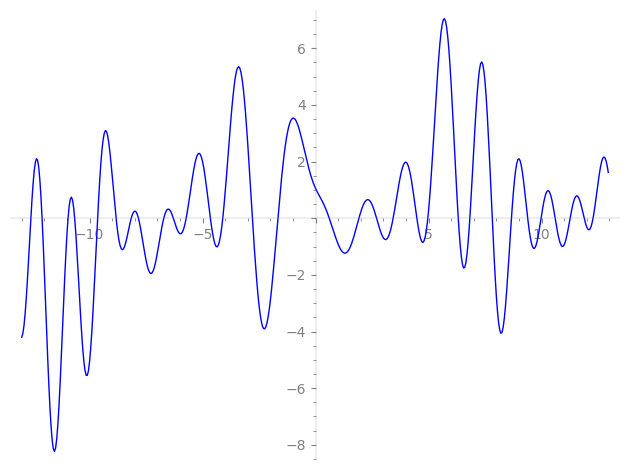
Imaginary part of the first few zeros on the critical line

−8.825222737480490100230818227444, −8.154570927242880399863047237480, −7.83745466537385128034347356573, −6.71546551106570761506650132229, −6.29259195118030257700162013294, −5.72388213842788098851298998120, −4.65317491767754539981333880651, −4.10556150031445727635030103659, −2.79407767424672084932317844664, −1.66656515019787610549979213440, 0.60509716381761286833321176178, 1.91836205548493902795633301186, 2.69867211466158488887812484968, 3.43224047465848575120971854693, 4.48122096768270992876452055487, 4.96673405790260399561103164244, 6.31324908031131142853839407029, 6.82577775678443202043494634617, 7.81729282935822541065844827956, 8.666534867949707468184752699091

Graph of the $Z$-function along the critical line