↑

Properties

Label 2-15e3-3.2-c0-0-6
Degree $2$
Conductor $3375$
Sign $1$
Analytic cond. $1.68434$
Root an. cond. $1.29782$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 1.82i·2-s − 2.33·4-s − 2.44i·8-s + 2.12·16-s − 1.95i·17-s − 1.82·19-s − 1.33i·23-s − 1.95·31-s + 1.44i·32-s + 3.57·34-s − 3.33i·38-s + 2.44·46-s − 1.61i·47-s − 49-s + 0.209i·53-s + ⋯
L(s)  = 1  + 1.82i·2-s − 2.33·4-s − 2.44i·8-s + 2.12·16-s − 1.95i·17-s − 1.82·19-s − 1.33i·23-s − 1.95·31-s + 1.44i·32-s + 3.57·34-s − 3.33i·38-s + 2.44·46-s − 1.61i·47-s − 49-s + 0.209i·53-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3375 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3375 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3375\)    =    \(3^{3} \cdot 5^{3}\)
Sign: $1$
Analytic conductor: \(1.68434\)
Root analytic conductor: \(1.29782\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3375} (1376, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3375,\ (\ :0),\ 1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.4934673226\)
\(L(\frac12)\) \(\approx\) \(0.4934673226\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 \)
5 \( 1 \)
good2 \( 1 - 1.82iT - T^{2} \)
7 \( 1 + T^{2} \)
11 \( 1 - T^{2} \)
13 \( 1 + T^{2} \)
17 \( 1 + 1.95iT - T^{2} \)
19 \( 1 + 1.82T + T^{2} \)
23 \( 1 + 1.33iT - T^{2} \)
29 \( 1 - T^{2} \)
31 \( 1 + 1.95T + T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 - T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 + 1.61iT - T^{2} \)
53 \( 1 - 0.209iT - T^{2} \)
59 \( 1 - T^{2} \)
61 \( 1 + 0.209T + T^{2} \)
67 \( 1 + T^{2} \)
71 \( 1 - T^{2} \)
73 \( 1 + T^{2} \)
79 \( 1 - 0.209T + T^{2} \)
83 \( 1 - 0.209iT - T^{2} \)
89 \( 1 - T^{2} \)
97 \( 1 + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

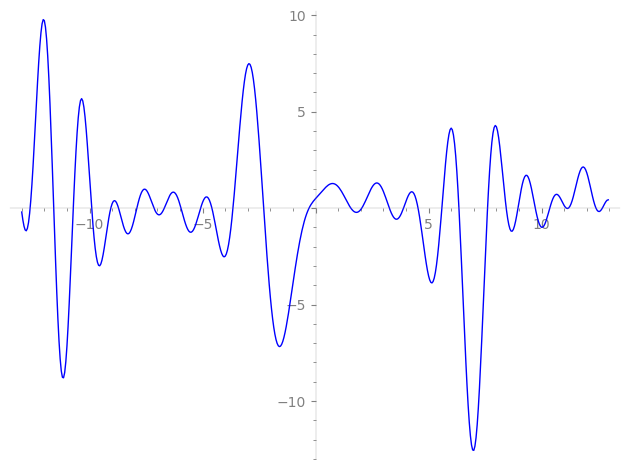
Imaginary part of the first few zeros on the critical line

−8.717264712716054537128525624295, −7.906527286251642073995642334849, −7.15106380006571344023232963896, −6.69214490164254775148805924891, −5.95420778777228819897130092559, −5.08489111882806646051148188378, −4.58733612137639498434243925582, −3.65401444200827237478620781999, −2.29642077818196458777941923242, −0.28790709775048257262888530787, 1.56062405406771046491979877722, 2.04440955693775002631801303930, 3.26461522100164185967484200541, 3.89168356983238406897511778764, 4.53367544624759941134443907771, 5.58742358961995843535992270371, 6.34305891947895765050659309041, 7.60876447986094351396841774604, 8.435397445188503102837135430982, 8.955515271445652244572887865592

Graph of the $Z$-function along the critical line