↑

Properties

Label 8-3549e4-1.1-c0e4-0-24
Degree 88
Conductor 1.586×10141.586\times 10^{14}
Sign 11
Analytic cond. 9.841309.84130
Root an. cond. 1.330851.33085
Motivic weight 00
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·3-s + 4·4-s + 9-s + 8·12-s + 10·16-s − 2·25-s − 2·27-s + 4·36-s − 2·43-s + 20·48-s + 49-s − 2·61-s + 20·64-s − 4·75-s + 4·79-s − 4·81-s − 8·100-s − 2·103-s − 8·108-s − 2·121-s + 127-s − 4·129-s + 131-s + 137-s + 139-s + 10·144-s + 2·147-s + ⋯
L(s)  = 1  + 2·3-s + 4·4-s + 9-s + 8·12-s + 10·16-s − 2·25-s − 2·27-s + 4·36-s − 2·43-s + 20·48-s + 49-s − 2·61-s + 20·64-s − 4·75-s + 4·79-s − 4·81-s − 8·100-s − 2·103-s − 8·108-s − 2·121-s + 127-s − 4·129-s + 131-s + 137-s + 139-s + 10·144-s + 2·147-s + ⋯

Functional equation

Λ(s)=((34⋅74⋅138)s/2 ΓC(s)4 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 7^{4} \cdot 13^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}
Λ(s)=((34⋅74⋅138)s/2 ΓC(s)4 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(3^{4} \cdot 7^{4} \cdot 13^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}

Invariants

Degree: 88
Conductor: 34⋅74⋅1383^{4} \cdot 7^{4} \cdot 13^{8}
Sign: 11
Analytic conductor: 9.841309.84130
Root analytic conductor: 1.330851.33085
Motivic weight: 00
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (8, 34⋅74⋅138, ( :0,0,0,0), 1)(8,\ 3^{4} \cdot 7^{4} \cdot 13^{8} ,\ ( \ : 0, 0, 0, 0 ),\ 1 )

Particular Values

L(12)L(\frac{1}{2}) ≈\approx 11.4842627811.48426278
L(12)L(\frac12) ≈\approx 11.4842627811.48426278
L(1)L(1) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad3C2C_2 (1−T+T2)2 ( 1 - T + T^{2} )^{2}
7C22C_2^2 1−T2+T4 1 - T^{2} + T^{4}
13 1 1
good2C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
5C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
11C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
17C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
19C2C_2×\timesC22C_2^2 (1+T2)2(1−T2+T4) ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} )
23C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
29C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
31C22C_2^2 (1−T2+T4)2 ( 1 - T^{2} + T^{4} )^{2}
37C22C_2^2 (1−T2+T4)2 ( 1 - T^{2} + T^{4} )^{2}
41C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
43C1C_1×\timesC2C_2 (1+T)4(1−T+T2)2 ( 1 + T )^{4}( 1 - T + T^{2} )^{2}
47C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
53C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
59C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
61C1C_1×\timesC2C_2 (1+T)4(1−T+T2)2 ( 1 + T )^{4}( 1 - T + T^{2} )^{2}
67C22C_2^2 (1−T2+T4)2 ( 1 - T^{2} + T^{4} )^{2}
71C2C_2 (1−T+T2)2(1+T+T2)2 ( 1 - T + T^{2} )^{2}( 1 + T + T^{2} )^{2}
73C2C_2×\timesC22C_2^2 (1+T2)2(1−T2+T4) ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} )
79C2C_2 (1−T+T2)4 ( 1 - T + T^{2} )^{4}
83C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
89C1C_1×\timesC1C_1 (1−T)4(1+T)4 ( 1 - T )^{4}( 1 + T )^{4}
97C2C_2×\timesC22C_2^2 (1+T2)2(1−T2+T4) ( 1 + T^{2} )^{2}( 1 - T^{2} + T^{4} )
show more
show less
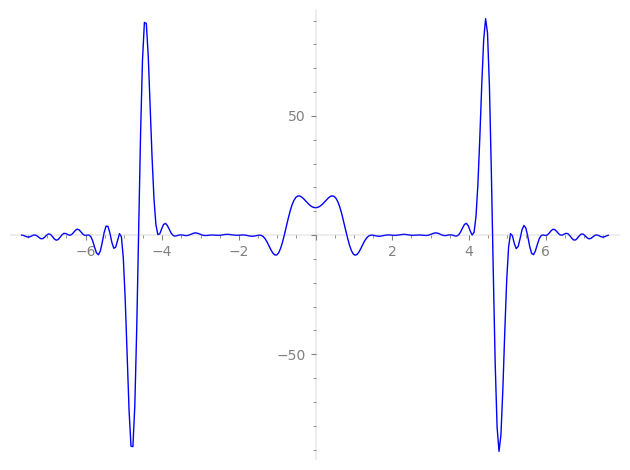
   L(s)=∏p ∏j=18(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−6.38732404658860027379510995027, −6.03915839678772079992509607185, −5.95249458955596928243037636377, −5.90163661378742136935363834672, −5.52867993822262665495069683566, −5.35363779109168185685981709906, −5.13001649403389599936093179948, −5.07343058786051468287813564611, −4.61730381879192338418289953927, −4.10490824913838260422917459534, −4.08606935045248576255948312038, −3.72640027700614220744431703369, −3.56977397857804554955629811244, −3.45935008746000476963276038698, −3.30505441354777963907830174650, −2.95093374238459842463127869838, −2.75829198716648536403476311878, −2.63836418199614725463343411497, −2.46498373550549570187149213201, −2.14375140428819996843764377047, −1.96862948860913271434557356564, −1.83657204359243327401382376216, −1.47581233420672987487139748645, −1.44758545457071734627694642464, −0.815561257211499001148503754492, 0.815561257211499001148503754492, 1.44758545457071734627694642464, 1.47581233420672987487139748645, 1.83657204359243327401382376216, 1.96862948860913271434557356564, 2.14375140428819996843764377047, 2.46498373550549570187149213201, 2.63836418199614725463343411497, 2.75829198716648536403476311878, 2.95093374238459842463127869838, 3.30505441354777963907830174650, 3.45935008746000476963276038698, 3.56977397857804554955629811244, 3.72640027700614220744431703369, 4.08606935045248576255948312038, 4.10490824913838260422917459534, 4.61730381879192338418289953927, 5.07343058786051468287813564611, 5.13001649403389599936093179948, 5.35363779109168185685981709906, 5.52867993822262665495069683566, 5.90163661378742136935363834672, 5.95249458955596928243037636377, 6.03915839678772079992509607185, 6.38732404658860027379510995027

Graph of the ZZ-function along the critical line