↑

Properties

Label 2-364-13.3-c1-0-4
Degree 22
Conductor 364364
Sign 0.964−0.265i0.964 - 0.265i
Analytic cond. 2.906552.90655
Root an. cond. 1.704861.70486
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.651 + 1.12i)3-s + 3.30·5-s + (0.5 − 0.866i)7-s + (0.651 − 1.12i)9-s + (−1.34 − 2.33i)11-s + (1.80 − 3.12i)13-s + (2.15 + 3.72i)15-s + (−2.80 + 4.85i)17-s + (−3.65 + 6.32i)19-s + 1.30·21-s + (−1 − 1.73i)23-s + 5.90·25-s + 5.60·27-s + (−1.65 − 2.86i)29-s − 7.60·31-s + ⋯
L(s)  = 1  + (0.376 + 0.651i)3-s + 1.47·5-s + (0.188 − 0.327i)7-s + (0.217 − 0.376i)9-s + (−0.406 − 0.704i)11-s + (0.499 − 0.866i)13-s + (0.555 + 0.962i)15-s + (−0.679 + 1.17i)17-s + (−0.837 + 1.45i)19-s + 0.284·21-s + (−0.208 − 0.361i)23-s + 1.18·25-s + 1.07·27-s + (−0.306 − 0.531i)29-s − 1.36·31-s + ⋯

Functional equation

Λ(s)=(364s/2 ΓC(s) L(s)=((0.964−0.265i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 364 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.964 - 0.265i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(364s/2 ΓC(s+1/2) L(s)=((0.964−0.265i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 364 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.964 - 0.265i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 364364    =    22⋅7⋅132^{2} \cdot 7 \cdot 13
Sign: 0.964−0.265i0.964 - 0.265i
Analytic conductor: 2.906552.90655
Root analytic conductor: 1.704861.70486
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ364(29,⋅)\chi_{364} (29, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 364, ( :1/2), 0.964−0.265i)(2,\ 364,\ (\ :1/2),\ 0.964 - 0.265i)

Particular Values

L(1)L(1) ≈\approx 1.87154+0.252500i1.87154 + 0.252500i
L(12)L(\frac12) ≈\approx 1.87154+0.252500i1.87154 + 0.252500i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
7 1+(−0.5+0.866i)T 1 + (-0.5 + 0.866i)T
13 1+(−1.80+3.12i)T 1 + (-1.80 + 3.12i)T
good3 1+(−0.651−1.12i)T+(−1.5+2.59i)T2 1 + (-0.651 - 1.12i)T + (-1.5 + 2.59i)T^{2}
5 1−3.30T+5T2 1 - 3.30T + 5T^{2}
11 1+(1.34+2.33i)T+(−5.5+9.52i)T2 1 + (1.34 + 2.33i)T + (-5.5 + 9.52i)T^{2}
17 1+(2.80−4.85i)T+(−8.5−14.7i)T2 1 + (2.80 - 4.85i)T + (-8.5 - 14.7i)T^{2}
19 1+(3.65−6.32i)T+(−9.5−16.4i)T2 1 + (3.65 - 6.32i)T + (-9.5 - 16.4i)T^{2}
23 1+(1+1.73i)T+(−11.5+19.9i)T2 1 + (1 + 1.73i)T + (-11.5 + 19.9i)T^{2}
29 1+(1.65+2.86i)T+(−14.5+25.1i)T2 1 + (1.65 + 2.86i)T + (-14.5 + 25.1i)T^{2}
31 1+7.60T+31T2 1 + 7.60T + 31T^{2}
37 1+(−2.60−4.51i)T+(−18.5+32.0i)T2 1 + (-2.60 - 4.51i)T + (-18.5 + 32.0i)T^{2}
41 1+(−4.30−7.45i)T+(−20.5+35.5i)T2 1 + (-4.30 - 7.45i)T + (-20.5 + 35.5i)T^{2}
43 1+(2.45−4.25i)T+(−21.5−37.2i)T2 1 + (2.45 - 4.25i)T + (-21.5 - 37.2i)T^{2}
47 1−4.39T+47T2 1 - 4.39T + 47T^{2}
53 1+10.8T+53T2 1 + 10.8T + 53T^{2}
59 1+(0.802−1.39i)T+(−29.5−51.0i)T2 1 + (0.802 - 1.39i)T + (-29.5 - 51.0i)T^{2}
61 1+(−3.60+6.24i)T+(−30.5−52.8i)T2 1 + (-3.60 + 6.24i)T + (-30.5 - 52.8i)T^{2}
67 1+(6.5+11.2i)T+(−33.5+58.0i)T2 1 + (6.5 + 11.2i)T + (-33.5 + 58.0i)T^{2}
71 1+(5.90−10.2i)T+(−35.5−61.4i)T2 1 + (5.90 - 10.2i)T + (-35.5 - 61.4i)T^{2}
73 1+3.21T+73T2 1 + 3.21T + 73T^{2}
79 1−8T+79T2 1 - 8T + 79T^{2}
83 1+11.6T+83T2 1 + 11.6T + 83T^{2}
89 1+(7.95+13.7i)T+(−44.5+77.0i)T2 1 + (7.95 + 13.7i)T + (-44.5 + 77.0i)T^{2}
97 1+(−8.45+14.6i)T+(−48.5−84.0i)T2 1 + (-8.45 + 14.6i)T + (-48.5 - 84.0i)T^{2}
show more
show less
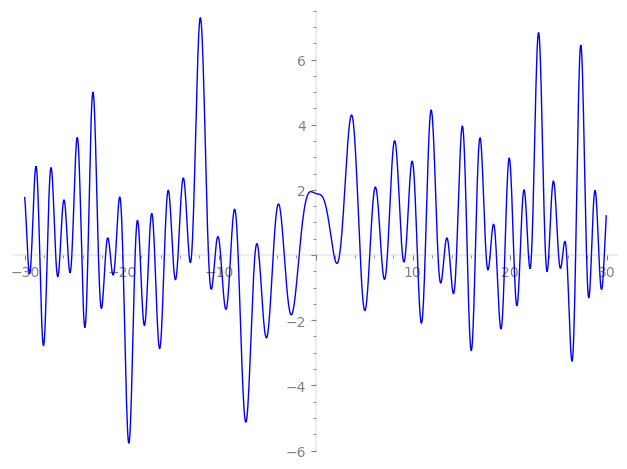
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.05674326327765276513777601910, −10.36973136255884811855218918198, −9.802451245183555581019388913908, −8.773312102873286037005101642550, −7.998800979577138175609824982962, −6.26535634696070366813830564331, −5.85481695330638953558994276287, −4.38344948311692887120068685202, −3.24183421362289111243489981232, −1.70663876683441375589242825840, 1.87620254324778795540896787179, 2.45436803452976693604073378195, 4.58464912842067791282364016506, 5.56754909329035572350907897989, 6.77196669989586514359521555106, 7.38596674438009953330486377799, 8.944072970333037794852033398344, 9.237574453228264165104829861674, 10.47980634173440490488121171393, 11.28228913789705753615892666988

Graph of the ZZ-function along the critical line