↑

Properties

Label 2-416-416.99-c1-0-8
Degree $2$
Conductor $416$
Sign $0.984 - 0.177i$
Analytic cond. $3.32177$
Root an. cond. $1.82257$
Motivic weight $1$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.717 − 1.21i)2-s + (0.172 − 0.415i)3-s + (−0.969 + 1.74i)4-s + (−0.252 + 0.610i)5-s + (−0.629 + 0.0885i)6-s − 3.40·7-s + (2.82 − 0.0751i)8-s + (1.97 + 1.97i)9-s + (0.925 − 0.130i)10-s + (−1.70 − 0.704i)11-s + (0.560 + 0.703i)12-s + (3.28 + 1.47i)13-s + (2.44 + 4.14i)14-s + (0.210 + 0.210i)15-s + (−2.12 − 3.39i)16-s + 2.30·17-s + ⋯
L(s)  = 1  + (−0.507 − 0.861i)2-s + (0.0993 − 0.239i)3-s + (−0.484 + 0.874i)4-s + (−0.113 + 0.272i)5-s + (−0.257 + 0.0361i)6-s − 1.28·7-s + (0.999 − 0.0265i)8-s + (0.659 + 0.659i)9-s + (0.292 − 0.0411i)10-s + (−0.512 − 0.212i)11-s + (0.161 + 0.203i)12-s + (0.912 + 0.410i)13-s + (0.652 + 1.10i)14-s + (0.0542 + 0.0542i)15-s + (−0.530 − 0.847i)16-s + 0.559·17-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 416 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.984 - 0.177i)\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 416 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.984 - 0.177i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(416\)    =    \(2^{5} \cdot 13\)
Sign: $0.984 - 0.177i$
Analytic conductor: \(3.32177\)
Root analytic conductor: \(1.82257\)
Motivic weight: \(1\)
Rational: no
Arithmetic: yes
Character: $\chi_{416} (99, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 416,\ (\ :1/2),\ 0.984 - 0.177i)\)

Particular Values

\(L(1)\) \(\approx\) \(0.877264 + 0.0785839i\)
\(L(\frac12)\) \(\approx\) \(0.877264 + 0.0785839i\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (0.717 + 1.21i)T \)
13 \( 1 + (-3.28 - 1.47i)T \)
good3 \( 1 + (-0.172 + 0.415i)T + (-2.12 - 2.12i)T^{2} \)
5 \( 1 + (0.252 - 0.610i)T + (-3.53 - 3.53i)T^{2} \)
7 \( 1 + 3.40T + 7T^{2} \)
11 \( 1 + (1.70 + 0.704i)T + (7.77 + 7.77i)T^{2} \)
17 \( 1 - 2.30T + 17T^{2} \)
19 \( 1 + (-2.92 - 7.05i)T + (-13.4 + 13.4i)T^{2} \)
23 \( 1 + (-1.96 - 1.96i)T + 23iT^{2} \)
29 \( 1 + (-0.820 - 0.339i)T + (20.5 + 20.5i)T^{2} \)
31 \( 1 + (1.78 - 1.78i)T - 31iT^{2} \)
37 \( 1 + (6.76 + 2.80i)T + (26.1 + 26.1i)T^{2} \)
41 \( 1 - 5.14iT - 41T^{2} \)
43 \( 1 + (-0.493 + 0.204i)T + (30.4 - 30.4i)T^{2} \)
47 \( 1 + (-1.59 + 1.59i)T - 47iT^{2} \)
53 \( 1 + (-5.87 + 2.43i)T + (37.4 - 37.4i)T^{2} \)
59 \( 1 + (-2.54 + 6.15i)T + (-41.7 - 41.7i)T^{2} \)
61 \( 1 + (5.74 + 2.37i)T + (43.1 + 43.1i)T^{2} \)
67 \( 1 + (2.69 - 1.11i)T + (47.3 - 47.3i)T^{2} \)
71 \( 1 - 7.20iT - 71T^{2} \)
73 \( 1 - 6.22T + 73T^{2} \)
79 \( 1 + 16.4T + 79T^{2} \)
83 \( 1 + (-0.384 - 0.929i)T + (-58.6 + 58.6i)T^{2} \)
89 \( 1 - 9.50iT - 89T^{2} \)
97 \( 1 + (8.56 + 8.56i)T + 97iT^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

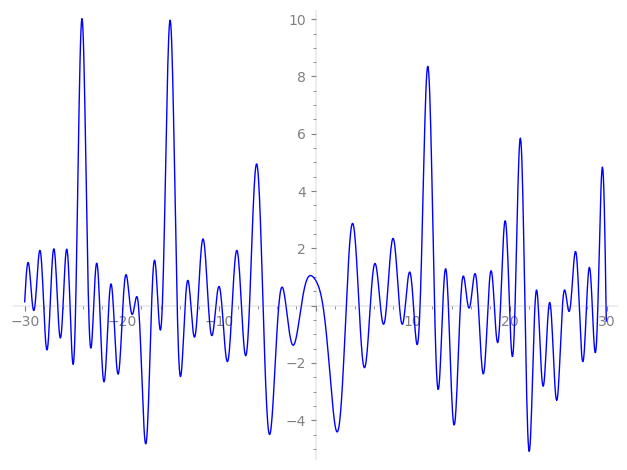
Imaginary part of the first few zeros on the critical line

−11.06169802841131362449239928102, −10.29169314916517795929867509054, −9.673991436024970400872308925928, −8.614418185004196079466429694811, −7.65644860739699845483178208165, −6.82469844329005342880997745907, −5.42637643006964263883042536029, −3.80713995409934219012046779173, −3.06842454212734969433620097236, −1.48570281467204913465669196117, 0.74365433081774179191023450742, 3.15146565932193268372512634530, 4.46697846270765032087950026493, 5.62681198963195930626749384267, 6.66393708526679060106879105453, 7.30149667870479653845565627372, 8.626567421799399314674416570286, 9.235355794820571090033356016303, 10.07387129274528481152397085944, 10.75509591270612247399470493642

Graph of the $Z$-function along the critical line