↑

Properties

Label 2-450-9.4-c1-0-6
Degree 22
Conductor 450450
Sign −0.173−0.984i-0.173 - 0.984i
Analytic cond. 3.593263.59326
Root an. cond. 1.895591.89559
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.5 + 0.866i)2-s + (1.5 + 0.866i)3-s + (−0.499 + 0.866i)4-s + 1.73i·6-s + (−0.5 − 0.866i)7-s − 0.999·8-s + (1.5 + 2.59i)9-s + (1 + 1.73i)11-s + (−1.49 + 0.866i)12-s + (−3 + 5.19i)13-s + (0.499 − 0.866i)14-s + (−0.5 − 0.866i)16-s + 2·17-s + (−1.5 + 2.59i)18-s + 6·19-s + ⋯
L(s)  = 1  + (0.353 + 0.612i)2-s + (0.866 + 0.499i)3-s + (−0.249 + 0.433i)4-s + 0.707i·6-s + (−0.188 − 0.327i)7-s − 0.353·8-s + (0.5 + 0.866i)9-s + (0.301 + 0.522i)11-s + (−0.433 + 0.250i)12-s + (−0.832 + 1.44i)13-s + (0.133 − 0.231i)14-s + (−0.125 − 0.216i)16-s + 0.485·17-s + (−0.353 + 0.612i)18-s + 1.37·19-s + ⋯

Functional equation

Λ(s)=(450s/2 ΓC(s) L(s)=((−0.173−0.984i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.173 - 0.984i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(450s/2 ΓC(s+1/2) L(s)=((−0.173−0.984i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.173 - 0.984i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 450450    =    2⋅32⋅522 \cdot 3^{2} \cdot 5^{2}
Sign: −0.173−0.984i-0.173 - 0.984i
Analytic conductor: 3.593263.59326
Root analytic conductor: 1.895591.89559
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ450(301,⋅)\chi_{450} (301, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 450, ( :1/2), −0.173−0.984i)(2,\ 450,\ (\ :1/2),\ -0.173 - 0.984i)

Particular Values

L(1)L(1) ≈\approx 1.34274+1.60022i1.34274 + 1.60022i
L(12)L(\frac12) ≈\approx 1.34274+1.60022i1.34274 + 1.60022i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−0.5−0.866i)T 1 + (-0.5 - 0.866i)T
3 1+(−1.5−0.866i)T 1 + (-1.5 - 0.866i)T
5 1 1
good7 1+(0.5+0.866i)T+(−3.5+6.06i)T2 1 + (0.5 + 0.866i)T + (-3.5 + 6.06i)T^{2}
11 1+(−1−1.73i)T+(−5.5+9.52i)T2 1 + (-1 - 1.73i)T + (-5.5 + 9.52i)T^{2}
13 1+(3−5.19i)T+(−6.5−11.2i)T2 1 + (3 - 5.19i)T + (-6.5 - 11.2i)T^{2}
17 1−2T+17T2 1 - 2T + 17T^{2}
19 1−6T+19T2 1 - 6T + 19T^{2}
23 1+(−0.5+0.866i)T+(−11.5−19.9i)T2 1 + (-0.5 + 0.866i)T + (-11.5 - 19.9i)T^{2}
29 1+(4.5+7.79i)T+(−14.5+25.1i)T2 1 + (4.5 + 7.79i)T + (-14.5 + 25.1i)T^{2}
31 1+(−1+1.73i)T+(−15.5−26.8i)T2 1 + (-1 + 1.73i)T + (-15.5 - 26.8i)T^{2}
37 1+2T+37T2 1 + 2T + 37T^{2}
41 1+(−5.5+9.52i)T+(−20.5−35.5i)T2 1 + (-5.5 + 9.52i)T + (-20.5 - 35.5i)T^{2}
43 1+(2+3.46i)T+(−21.5+37.2i)T2 1 + (2 + 3.46i)T + (-21.5 + 37.2i)T^{2}
47 1+(3.5+6.06i)T+(−23.5+40.7i)T2 1 + (3.5 + 6.06i)T + (-23.5 + 40.7i)T^{2}
53 1+53T2 1 + 53T^{2}
59 1+(−2+3.46i)T+(−29.5−51.0i)T2 1 + (-2 + 3.46i)T + (-29.5 - 51.0i)T^{2}
61 1+(−3.5−6.06i)T+(−30.5+52.8i)T2 1 + (-3.5 - 6.06i)T + (-30.5 + 52.8i)T^{2}
67 1+(5.5−9.52i)T+(−33.5−58.0i)T2 1 + (5.5 - 9.52i)T + (-33.5 - 58.0i)T^{2}
71 1+6T+71T2 1 + 6T + 71T^{2}
73 1−4T+73T2 1 - 4T + 73T^{2}
79 1+(−6−10.3i)T+(−39.5+68.4i)T2 1 + (-6 - 10.3i)T + (-39.5 + 68.4i)T^{2}
83 1+(5.5+9.52i)T+(−41.5+71.8i)T2 1 + (5.5 + 9.52i)T + (-41.5 + 71.8i)T^{2}
89 1−T+89T2 1 - T + 89T^{2}
97 1+(4+6.92i)T+(−48.5+84.0i)T2 1 + (4 + 6.92i)T + (-48.5 + 84.0i)T^{2}
show more
show less
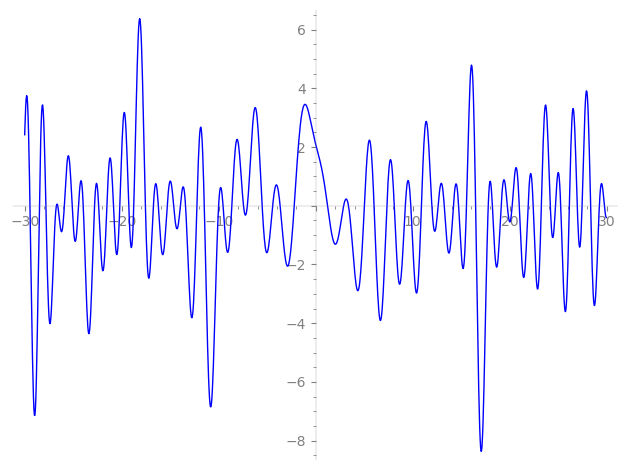
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.48966756677868233448556566790, −10.01017730899387037747275254222, −9.550844405896477565828687250390, −8.648292995987210437224674686512, −7.44251812564754360861457906003, −7.04986705036110303408472636946, −5.52079711748507274723474061707, −4.43777152634048219273672562745, −3.66955792786175549294448284817, −2.21546056966703936744975929825, 1.21655190000704858499829476092, 2.87865039617803272921413129887, 3.37561479560052560478036735673, 5.01338013227043856912891670704, 6.01346710259467282913268356923, 7.33363924584719492375648275269, 8.097339354425975875850425490863, 9.236182684772098707220787825060, 9.801225634631384391720901245147, 10.89494979573783573752794986184

Graph of the ZZ-function along the critical line