↑

Properties

Label 2-567-63.4-c1-0-29
Degree 22
Conductor 567567
Sign −0.474−0.880i-0.474 - 0.880i
Analytic cond. 4.527514.52751
Root an. cond. 2.127792.12779
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.29 − 2.24i)2-s + (−2.34 − 4.06i)4-s − 2.28·5-s + (−2.08 − 1.63i)7-s − 6.97·8-s + (−2.95 + 5.11i)10-s + 2.95·11-s + (−2.13 + 3.69i)13-s + (−6.34 + 2.56i)14-s + (−4.32 + 7.49i)16-s + (−0.764 + 1.32i)17-s + (−3.69 − 6.39i)19-s + (5.35 + 9.28i)20-s + (3.82 − 6.62i)22-s + 6.15·23-s + ⋯
L(s)  = 1  + (0.914 − 1.58i)2-s + (−1.17 − 2.03i)4-s − 1.02·5-s + (−0.787 − 0.616i)7-s − 2.46·8-s + (−0.934 + 1.61i)10-s + 0.891·11-s + (−0.591 + 1.02i)13-s + (−1.69 + 0.684i)14-s + (−1.08 + 1.87i)16-s + (−0.185 + 0.321i)17-s + (−0.846 − 1.46i)19-s + (1.19 + 2.07i)20-s + (0.815 − 1.41i)22-s + 1.28·23-s + ⋯

Functional equation

Λ(s)=(567s/2 ΓC(s) L(s)=((−0.474−0.880i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 567 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.474 - 0.880i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(567s/2 ΓC(s+1/2) L(s)=((−0.474−0.880i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 567 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.474 - 0.880i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 567567    =    34⋅73^{4} \cdot 7
Sign: −0.474−0.880i-0.474 - 0.880i
Analytic conductor: 4.527514.52751
Root analytic conductor: 2.127792.12779
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ567(109,⋅)\chi_{567} (109, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 567, ( :1/2), −0.474−0.880i)(2,\ 567,\ (\ :1/2),\ -0.474 - 0.880i)

Particular Values

L(1)L(1) ≈\approx 0.535648+0.897340i0.535648 + 0.897340i
L(12)L(\frac12) ≈\approx 0.535648+0.897340i0.535648 + 0.897340i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1 1
7 1+(2.08+1.63i)T 1 + (2.08 + 1.63i)T
good2 1+(−1.29+2.24i)T+(−1−1.73i)T2 1 + (-1.29 + 2.24i)T + (-1 - 1.73i)T^{2}
5 1+2.28T+5T2 1 + 2.28T + 5T^{2}
11 1−2.95T+11T2 1 - 2.95T + 11T^{2}
13 1+(2.13−3.69i)T+(−6.5−11.2i)T2 1 + (2.13 - 3.69i)T + (-6.5 - 11.2i)T^{2}
17 1+(0.764−1.32i)T+(−8.5−14.7i)T2 1 + (0.764 - 1.32i)T + (-8.5 - 14.7i)T^{2}
19 1+(3.69+6.39i)T+(−9.5+16.4i)T2 1 + (3.69 + 6.39i)T + (-9.5 + 16.4i)T^{2}
23 1−6.15T+23T2 1 - 6.15T + 23T^{2}
29 1+(1.17+2.02i)T+(−14.5+25.1i)T2 1 + (1.17 + 2.02i)T + (-14.5 + 25.1i)T^{2}
31 1+(3.11+5.38i)T+(−15.5+26.8i)T2 1 + (3.11 + 5.38i)T + (-15.5 + 26.8i)T^{2}
37 1+(3.58+6.21i)T+(−18.5+32.0i)T2 1 + (3.58 + 6.21i)T + (-18.5 + 32.0i)T^{2}
41 1+(3.94−6.83i)T+(−20.5−35.5i)T2 1 + (3.94 - 6.83i)T + (-20.5 - 35.5i)T^{2}
43 1+(0.417+0.722i)T+(−21.5+37.2i)T2 1 + (0.417 + 0.722i)T + (-21.5 + 37.2i)T^{2}
47 1+(−2.91+5.04i)T+(−23.5−40.7i)T2 1 + (-2.91 + 5.04i)T + (-23.5 - 40.7i)T^{2}
53 1+(−3.71+6.44i)T+(−26.5−45.8i)T2 1 + (-3.71 + 6.44i)T + (-26.5 - 45.8i)T^{2}
59 1+(2.31+4.00i)T+(−29.5+51.0i)T2 1 + (2.31 + 4.00i)T + (-29.5 + 51.0i)T^{2}
61 1+(−3.56+6.17i)T+(−30.5−52.8i)T2 1 + (-3.56 + 6.17i)T + (-30.5 - 52.8i)T^{2}
67 1+(−1.66−2.87i)T+(−33.5+58.0i)T2 1 + (-1.66 - 2.87i)T + (-33.5 + 58.0i)T^{2}
71 1+0.160T+71T2 1 + 0.160T + 71T^{2}
73 1+(−0.190+0.329i)T+(−36.5−63.2i)T2 1 + (-0.190 + 0.329i)T + (-36.5 - 63.2i)T^{2}
79 1+(−3.97+6.88i)T+(−39.5−68.4i)T2 1 + (-3.97 + 6.88i)T + (-39.5 - 68.4i)T^{2}
83 1+(−2.14−3.72i)T+(−41.5+71.8i)T2 1 + (-2.14 - 3.72i)T + (-41.5 + 71.8i)T^{2}
89 1+(3.02+5.24i)T+(−44.5+77.0i)T2 1 + (3.02 + 5.24i)T + (-44.5 + 77.0i)T^{2}
97 1+(−0.661−1.14i)T+(−48.5+84.0i)T2 1 + (-0.661 - 1.14i)T + (-48.5 + 84.0i)T^{2}
show more
show less
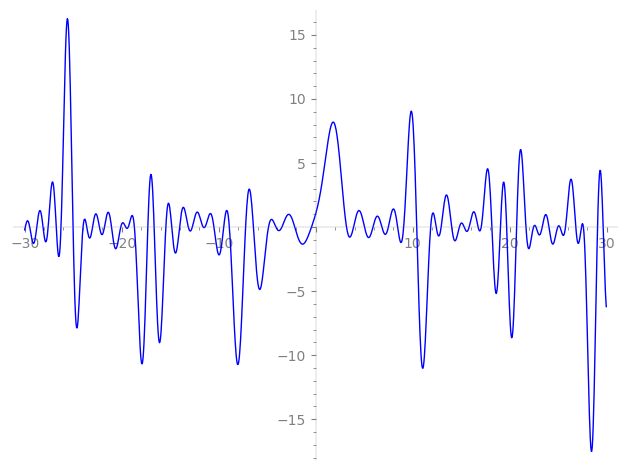
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.49058872240353760305658951696, −9.485870412010980895302343287764, −8.905238614689408033666105350117, −7.22957716594408565108386377579, −6.42377487089434661090435755488, −4.86843804450759544720056239592, −4.10107073509334457562733514498, −3.48444940943811202632110840672, −2.16232306959341417980756373950, −0.43598902480773177547188798239, 3.17448927382438564620306559757, 3.89824043188633756207852877932, 5.02877255570607615551498141621, 5.90117261763225180139346086875, 6.82156369083884168371378790030, 7.48690663581172456090797017230, 8.444873437880269726162909753881, 9.064408036808993966817980561781, 10.41195479304186732316196214635, 11.84877300164264630758833268202

Graph of the ZZ-function along the critical line