↑

Properties

Label 4-567e2-1.1-c1e2-0-25
Degree 44
Conductor 321489321489
Sign 11
Analytic cond. 20.498420.4984
Root an. cond. 2.127792.12779
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 4·4-s + 4·7-s + 3·13-s + 12·16-s − 9·19-s + 5·25-s + 16·28-s − 37-s + 5·43-s + 9·49-s + 12·52-s + 32·64-s + 22·67-s − 27·73-s − 36·76-s − 26·79-s + 12·91-s − 24·97-s + 20·100-s − 33·103-s + 17·109-s + 48·112-s − 11·121-s + 127-s + 131-s − 36·133-s + 137-s + ⋯
L(s)  = 1  + 2·4-s + 1.51·7-s + 0.832·13-s + 3·16-s − 2.06·19-s + 25-s + 3.02·28-s − 0.164·37-s + 0.762·43-s + 9/7·49-s + 1.66·52-s + 4·64-s + 2.68·67-s − 3.16·73-s − 4.12·76-s − 2.92·79-s + 1.25·91-s − 2.43·97-s + 2·100-s − 3.25·103-s + 1.62·109-s + 4.53·112-s − 121-s + 0.0887·127-s + 0.0873·131-s − 3.12·133-s + 0.0854·137-s + ⋯

Functional equation

Λ(s)=(321489s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 321489 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(321489s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 321489 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 321489321489    =    38⋅723^{8} \cdot 7^{2}
Sign: 11
Analytic conductor: 20.498420.4984
Root analytic conductor: 2.127792.12779
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 321489, ( :1/2,1/2), 1)(4,\ 321489,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 3.9084670813.908467081
L(12)L(\frac12) ≈\approx 3.9084670813.908467081
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad3 1 1
7C2C_2 1−4T+pT2 1 - 4 T + p T^{2}
good2C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
5C22C_2^2 1−pT2+p2T4 1 - p T^{2} + p^{2} T^{4}
11C22C_2^2 1+pT2+p2T4 1 + p T^{2} + p^{2} T^{4}
13C2C_2 (1−5T+pT2)(1+2T+pT2) ( 1 - 5 T + p T^{2} )( 1 + 2 T + p T^{2} )
17C22C_2^2 1−pT2+p2T4 1 - p T^{2} + p^{2} T^{4}
19C2C_2 (1+T+pT2)(1+8T+pT2) ( 1 + T + p T^{2} )( 1 + 8 T + p T^{2} )
23C22C_2^2 1+pT2+p2T4 1 + p T^{2} + p^{2} T^{4}
29C22C_2^2 1+pT2+p2T4 1 + p T^{2} + p^{2} T^{4}
31C2C_2 (1−7T+pT2)(1+7T+pT2) ( 1 - 7 T + p T^{2} )( 1 + 7 T + p T^{2} )
37C2C_2 (1−10T+pT2)(1+11T+pT2) ( 1 - 10 T + p T^{2} )( 1 + 11 T + p T^{2} )
41C22C_2^2 1−pT2+p2T4 1 - p T^{2} + p^{2} T^{4}
43C2C_2 (1−13T+pT2)(1+8T+pT2) ( 1 - 13 T + p T^{2} )( 1 + 8 T + p T^{2} )
47C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
53C22C_2^2 1+pT2+p2T4 1 + p T^{2} + p^{2} T^{4}
59C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
61C2C_2 (1−14T+pT2)(1+14T+pT2) ( 1 - 14 T + p T^{2} )( 1 + 14 T + p T^{2} )
67C2C_2 (1−11T+pT2)2 ( 1 - 11 T + p T^{2} )^{2}
71C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
73C2C_2 (1+10T+pT2)(1+17T+pT2) ( 1 + 10 T + p T^{2} )( 1 + 17 T + p T^{2} )
79C2C_2 (1+13T+pT2)2 ( 1 + 13 T + p T^{2} )^{2}
83C22C_2^2 1−pT2+p2T4 1 - p T^{2} + p^{2} T^{4}
89C22C_2^2 1−pT2+p2T4 1 - p T^{2} + p^{2} T^{4}
97C2C_2 (1+5T+pT2)(1+19T+pT2) ( 1 + 5 T + p T^{2} )( 1 + 19 T + p T^{2} )
show more
show less
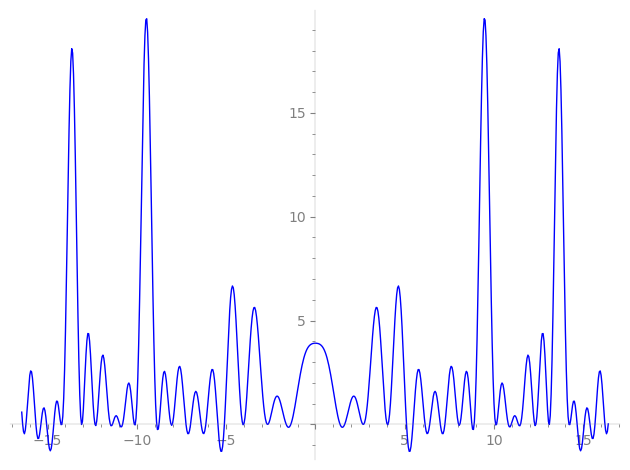
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.96640617341950846294003090899, −10.80160183622685390093008698612, −10.14675132633544754035340080738, −10.09037317724438320334506883848, −8.888586260839942921327067006715, −8.761570856361985341027472109431, −8.089800982392398156268615062530, −8.017048840680845066199579534820, −7.24957862861028457395485576462, −6.99457579740512571164538674499, −6.39914518115292003908587222515, −6.13944624876711242862314085014, −5.46350057918716772869735603377, −5.10101186800904647040691920912, −4.06430820569097814351182259876, −4.01687775311236423892081915788, −2.69891741342343106192034128999, −2.65823283055454640986641600539, −1.63767714876374694294915229184, −1.37815594620778404487983892563, 1.37815594620778404487983892563, 1.63767714876374694294915229184, 2.65823283055454640986641600539, 2.69891741342343106192034128999, 4.01687775311236423892081915788, 4.06430820569097814351182259876, 5.10101186800904647040691920912, 5.46350057918716772869735603377, 6.13944624876711242862314085014, 6.39914518115292003908587222515, 6.99457579740512571164538674499, 7.24957862861028457395485576462, 8.017048840680845066199579534820, 8.089800982392398156268615062530, 8.761570856361985341027472109431, 8.888586260839942921327067006715, 10.09037317724438320334506883848, 10.14675132633544754035340080738, 10.80160183622685390093008698612, 10.96640617341950846294003090899

Graph of the ZZ-function along the critical line