↑

Properties

Label 2-588-7.4-c3-0-7
Degree 22
Conductor 588588
Sign 0.991−0.126i0.991 - 0.126i
Analytic cond. 34.693134.6931
Root an. cond. 5.890085.89008
Motivic weight 33
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.5 − 2.59i)3-s + (−3 − 5.19i)5-s + (−4.5 − 7.79i)9-s + (−18 + 31.1i)11-s + 62·13-s − 18·15-s + (−57 + 98.7i)17-s + (38 + 65.8i)19-s + (12 + 20.7i)23-s + (44.5 − 77.0i)25-s − 27·27-s + 54·29-s + (56 − 96.9i)31-s + (54 + 93.5i)33-s + (89 + 154. i)37-s + ⋯
L(s)  = 1  + (0.288 − 0.499i)3-s + (−0.268 − 0.464i)5-s + (−0.166 − 0.288i)9-s + (−0.493 + 0.854i)11-s + 1.32·13-s − 0.309·15-s + (−0.813 + 1.40i)17-s + (0.458 + 0.794i)19-s + (0.108 + 0.188i)23-s + (0.355 − 0.616i)25-s − 0.192·27-s + 0.345·29-s + (0.324 − 0.561i)31-s + (0.284 + 0.493i)33-s + (0.395 + 0.684i)37-s + ⋯

Functional equation

Λ(s)=(588s/2 ΓC(s) L(s)=((0.991−0.126i) Λ‾(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 588 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.991 - 0.126i)\, \overline{\Lambda}(4-s) \end{aligned}
Λ(s)=(588s/2 ΓC(s+3/2) L(s)=((0.991−0.126i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 588 ^{s/2} \, \Gamma_{\C}(s+3/2) \, L(s)\cr =\mathstrut & (0.991 - 0.126i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 588588    =    22⋅3⋅722^{2} \cdot 3 \cdot 7^{2}
Sign: 0.991−0.126i0.991 - 0.126i
Analytic conductor: 34.693134.6931
Root analytic conductor: 5.890085.89008
Motivic weight: 33
Rational: no
Arithmetic: yes
Character: χ588(361,⋅)\chi_{588} (361, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 588, ( :3/2), 0.991−0.126i)(2,\ 588,\ (\ :3/2),\ 0.991 - 0.126i)

Particular Values

L(2)L(2) ≈\approx 1.9999269331.999926933
L(12)L(\frac12) ≈\approx 1.9999269331.999926933
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
3 1+(−1.5+2.59i)T 1 + (-1.5 + 2.59i)T
7 1 1
good5 1+(3+5.19i)T+(−62.5+108.i)T2 1 + (3 + 5.19i)T + (-62.5 + 108. i)T^{2}
11 1+(18−31.1i)T+(−665.5−1.15e3i)T2 1 + (18 - 31.1i)T + (-665.5 - 1.15e3i)T^{2}
13 1−62T+2.19e3T2 1 - 62T + 2.19e3T^{2}
17 1+(57−98.7i)T+(−2.45e3−4.25e3i)T2 1 + (57 - 98.7i)T + (-2.45e3 - 4.25e3i)T^{2}
19 1+(−38−65.8i)T+(−3.42e3+5.94e3i)T2 1 + (-38 - 65.8i)T + (-3.42e3 + 5.94e3i)T^{2}
23 1+(−12−20.7i)T+(−6.08e3+1.05e4i)T2 1 + (-12 - 20.7i)T + (-6.08e3 + 1.05e4i)T^{2}
29 1−54T+2.43e4T2 1 - 54T + 2.43e4T^{2}
31 1+(−56+96.9i)T+(−1.48e4−2.57e4i)T2 1 + (-56 + 96.9i)T + (-1.48e4 - 2.57e4i)T^{2}
37 1+(−89−154.i)T+(−2.53e4+4.38e4i)T2 1 + (-89 - 154. i)T + (-2.53e4 + 4.38e4i)T^{2}
41 1−378T+6.89e4T2 1 - 378T + 6.89e4T^{2}
43 1+172T+7.95e4T2 1 + 172T + 7.95e4T^{2}
47 1+(−96−166.i)T+(−5.19e4+8.99e4i)T2 1 + (-96 - 166. i)T + (-5.19e4 + 8.99e4i)T^{2}
53 1+(−201+348.i)T+(−7.44e4−1.28e5i)T2 1 + (-201 + 348. i)T + (-7.44e4 - 1.28e5i)T^{2}
59 1+(198−342.i)T+(−1.02e5−1.77e5i)T2 1 + (198 - 342. i)T + (-1.02e5 - 1.77e5i)T^{2}
61 1+(127+219.i)T+(−1.13e5+1.96e5i)T2 1 + (127 + 219. i)T + (-1.13e5 + 1.96e5i)T^{2}
67 1+(−506+876.i)T+(−1.50e5−2.60e5i)T2 1 + (-506 + 876. i)T + (-1.50e5 - 2.60e5i)T^{2}
71 1−840T+3.57e5T2 1 - 840T + 3.57e5T^{2}
73 1+(445−770.i)T+(−1.94e5−3.36e5i)T2 1 + (445 - 770. i)T + (-1.94e5 - 3.36e5i)T^{2}
79 1+(40+69.2i)T+(−2.46e5+4.26e5i)T2 1 + (40 + 69.2i)T + (-2.46e5 + 4.26e5i)T^{2}
83 1+108T+5.71e5T2 1 + 108T + 5.71e5T^{2}
89 1+(−819−1.41e3i)T+(−3.52e5+6.10e5i)T2 1 + (-819 - 1.41e3i)T + (-3.52e5 + 6.10e5i)T^{2}
97 1−1.01e3T+9.12e5T2 1 - 1.01e3T + 9.12e5T^{2}
show more
show less
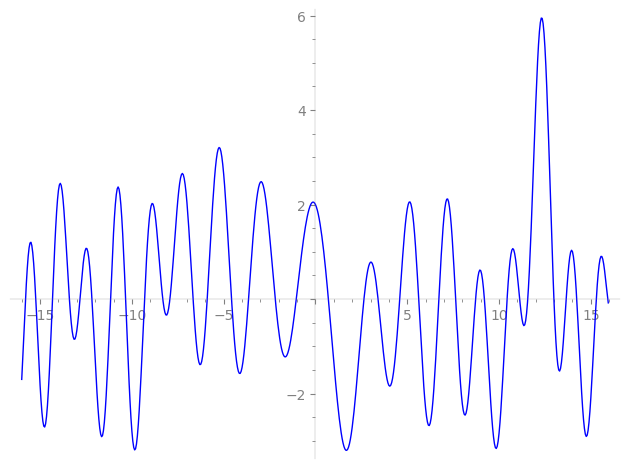
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.34174629931237729699295735139, −9.311068297514870732874332506337, −8.315435924673506184705901777386, −7.929220549369215699759890307832, −6.66408121993122525124579538940, −5.89686915307238029727336224857, −4.57114510849333380922032992217, −3.64526255287665601643947235567, −2.18963247758081236365328139228, −1.04513199505327350551756372369, 0.70400936715459271855989799689, 2.64186921580646056510437268567, 3.40958740376852595099529052475, 4.58893211114418084095480274218, 5.62368610635681146210563997563, 6.72164535406600568040459253198, 7.63643308295150064124814948595, 8.723159257847745853314694919191, 9.201642206615003951774789274010, 10.43865124935574997480352694096

Graph of the ZZ-function along the critical line