↑

Properties

Label 2-59-59.58-c6-0-13
Degree 22
Conductor 5959
Sign −0.423+0.905i-0.423 + 0.905i
Analytic cond. 13.573113.5731
Root an. cond. 3.684183.68418
Motivic weight 66
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 11.1i·2-s − 46.4·3-s − 59.3·4-s + 157.·5-s + 516. i·6-s + 407.·7-s − 51.1i·8-s + 1.43e3·9-s − 1.75e3i·10-s + 2.36e3i·11-s + 2.76e3·12-s − 1.83e3i·13-s − 4.53e3i·14-s − 7.34e3·15-s − 4.36e3·16-s + 1.70e3·17-s + ⋯
L(s)  = 1  − 1.38i·2-s − 1.72·3-s − 0.928·4-s + 1.26·5-s + 2.39i·6-s + 1.18·7-s − 0.0999i·8-s + 1.96·9-s − 1.75i·10-s + 1.77i·11-s + 1.59·12-s − 0.835i·13-s − 1.65i·14-s − 2.17·15-s − 1.06·16-s + 0.347·17-s + ⋯

Functional equation

Λ(s)=(59s/2 ΓC(s) L(s)=((−0.423+0.905i) Λ‾(7−s)\begin{aligned}\Lambda(s)=\mathstrut & 59 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.423 + 0.905i)\, \overline{\Lambda}(7-s) \end{aligned}
Λ(s)=(59s/2 ΓC(s+3) L(s)=((−0.423+0.905i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 59 ^{s/2} \, \Gamma_{\C}(s+3) \, L(s)\cr =\mathstrut & (-0.423 + 0.905i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 5959
Sign: −0.423+0.905i-0.423 + 0.905i
Analytic conductor: 13.573113.5731
Root analytic conductor: 3.684183.68418
Motivic weight: 66
Rational: no
Arithmetic: yes
Character: χ59(58,⋅)\chi_{59} (58, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 59, ( :3), −0.423+0.905i)(2,\ 59,\ (\ :3),\ -0.423 + 0.905i)

Particular Values

L(72)L(\frac{7}{2}) ≈\approx 0.797907−1.25451i0.797907 - 1.25451i
L(12)L(\frac12) ≈\approx 0.797907−1.25451i0.797907 - 1.25451i
L(4)L(4) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad59 1+(−8.70e4+1.86e5i)T 1 + (-8.70e4 + 1.86e5i)T
good2 1+11.1iT−64T2 1 + 11.1iT - 64T^{2}
3 1+46.4T+729T2 1 + 46.4T + 729T^{2}
5 1−157.T+1.56e4T2 1 - 157.T + 1.56e4T^{2}
7 1−407.T+1.17e5T2 1 - 407.T + 1.17e5T^{2}
11 1−2.36e3iT−1.77e6T2 1 - 2.36e3iT - 1.77e6T^{2}
13 1+1.83e3iT−4.82e6T2 1 + 1.83e3iT - 4.82e6T^{2}
17 1−1.70e3T+2.41e7T2 1 - 1.70e3T + 2.41e7T^{2}
19 1−1.01e4T+4.70e7T2 1 - 1.01e4T + 4.70e7T^{2}
23 1+1.16e4iT−1.48e8T2 1 + 1.16e4iT - 1.48e8T^{2}
29 1−5.12e3T+5.94e8T2 1 - 5.12e3T + 5.94e8T^{2}
31 1−1.89e4iT−8.87e8T2 1 - 1.89e4iT - 8.87e8T^{2}
37 1+9.20e4iT−2.56e9T2 1 + 9.20e4iT - 2.56e9T^{2}
41 1−7.36e4T+4.75e9T2 1 - 7.36e4T + 4.75e9T^{2}
43 1−5.20e3iT−6.32e9T2 1 - 5.20e3iT - 6.32e9T^{2}
47 1+7.90e4iT−1.07e10T2 1 + 7.90e4iT - 1.07e10T^{2}
53 1+1.32e5T+2.21e10T2 1 + 1.32e5T + 2.21e10T^{2}
61 1−2.06e5iT−5.15e10T2 1 - 2.06e5iT - 5.15e10T^{2}
67 1−3.66e5iT−9.04e10T2 1 - 3.66e5iT - 9.04e10T^{2}
71 1−6.82e5T+1.28e11T2 1 - 6.82e5T + 1.28e11T^{2}
73 1−1.32e4iT−1.51e11T2 1 - 1.32e4iT - 1.51e11T^{2}
79 1+4.18e5T+2.43e11T2 1 + 4.18e5T + 2.43e11T^{2}
83 1−5.57e4iT−3.26e11T2 1 - 5.57e4iT - 3.26e11T^{2}
89 1+1.20e6iT−4.96e11T2 1 + 1.20e6iT - 4.96e11T^{2}
97 1+1.41e5iT−8.32e11T2 1 + 1.41e5iT - 8.32e11T^{2}
show more
show less
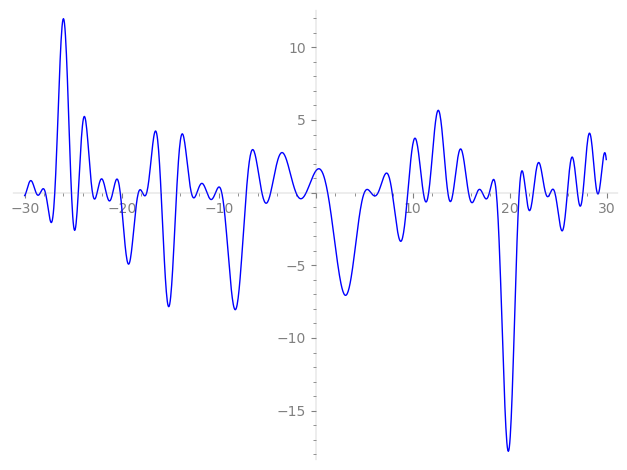
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.82439041886556220669546059543, −12.24478162939522818138915615489, −11.21261679745340911140290230017, −10.32550493445283692085184671623, −9.687385165576239902356227464997, −7.16255698612963749523875609218, −5.54869536452045317509234837978, −4.64712903698493702752979245743, −2.03755499453992696242291846095, −0.985037163490887919361031882775, 1.23052924848523117004542016202, 5.00971882997659305124709334685, 5.69041583533323128071158577049, 6.43123533069457545046283511626, 7.88086612476645624934462227265, 9.488991151789635106375013558955, 11.09181233466197071692612212874, 11.63988912624347906370839132513, 13.62029181168321534776860756931, 14.15715574736590079574872061008

Graph of the ZZ-function along the critical line