↑

Properties

Label 2-637-91.45-c1-0-35
Degree 22
Conductor 637637
Sign 0.656+0.754i0.656 + 0.754i
Analytic cond. 5.086475.08647
Root an. cond. 2.255322.25532
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.65 + 1.65i)2-s + (2.39 − 1.38i)3-s − 3.50i·4-s + (0.412 − 1.53i)5-s + (−1.67 + 6.25i)6-s + (2.50 + 2.50i)8-s + (2.30 − 4.00i)9-s + (1.87 + 3.23i)10-s + (0.813 − 3.03i)11-s + (−4.84 − 8.39i)12-s + (−1.04 − 3.44i)13-s + (−1.13 − 4.24i)15-s − 1.29·16-s − 0.641·17-s + (2.80 + 10.4i)18-s + (−7.61 + 2.04i)19-s + ⋯
L(s)  = 1  + (−1.17 + 1.17i)2-s + (1.38 − 0.796i)3-s − 1.75i·4-s + (0.184 − 0.688i)5-s + (−0.684 + 2.55i)6-s + (0.886 + 0.886i)8-s + (0.769 − 1.33i)9-s + (0.591 + 1.02i)10-s + (0.245 − 0.914i)11-s + (−1.39 − 2.42i)12-s + (−0.290 − 0.956i)13-s + (−0.293 − 1.09i)15-s − 0.324·16-s − 0.155·17-s + (0.661 + 2.46i)18-s + (−1.74 + 0.468i)19-s + ⋯

Functional equation

Λ(s)=(637s/2 ΓC(s) L(s)=((0.656+0.754i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.656 + 0.754i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(637s/2 ΓC(s+1/2) L(s)=((0.656+0.754i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.656 + 0.754i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 637637    =    72⋅137^{2} \cdot 13
Sign: 0.656+0.754i0.656 + 0.754i
Analytic conductor: 5.086475.08647
Root analytic conductor: 2.255322.25532
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ637(227,⋅)\chi_{637} (227, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 637, ( :1/2), 0.656+0.754i)(2,\ 637,\ (\ :1/2),\ 0.656 + 0.754i)

Particular Values

L(1)L(1) ≈\approx 1.06748−0.485816i1.06748 - 0.485816i
L(12)L(\frac12) ≈\approx 1.06748−0.485816i1.06748 - 0.485816i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad7 1 1
13 1+(1.04+3.44i)T 1 + (1.04 + 3.44i)T
good2 1+(1.65−1.65i)T−2iT2 1 + (1.65 - 1.65i)T - 2iT^{2}
3 1+(−2.39+1.38i)T+(1.5−2.59i)T2 1 + (-2.39 + 1.38i)T + (1.5 - 2.59i)T^{2}
5 1+(−0.412+1.53i)T+(−4.33−2.5i)T2 1 + (-0.412 + 1.53i)T + (-4.33 - 2.5i)T^{2}
11 1+(−0.813+3.03i)T+(−9.52−5.5i)T2 1 + (-0.813 + 3.03i)T + (-9.52 - 5.5i)T^{2}
17 1+0.641T+17T2 1 + 0.641T + 17T^{2}
19 1+(7.61−2.04i)T+(16.4−9.5i)T2 1 + (7.61 - 2.04i)T + (16.4 - 9.5i)T^{2}
23 1−0.146iT−23T2 1 - 0.146iT - 23T^{2}
29 1+(−1.49+2.58i)T+(−14.5−25.1i)T2 1 + (-1.49 + 2.58i)T + (-14.5 - 25.1i)T^{2}
31 1+(6.46−1.73i)T+(26.8−15.5i)T2 1 + (6.46 - 1.73i)T + (26.8 - 15.5i)T^{2}
37 1+(2.75+2.75i)T+37iT2 1 + (2.75 + 2.75i)T + 37iT^{2}
41 1+(−5.60+1.50i)T+(35.5−20.5i)T2 1 + (-5.60 + 1.50i)T + (35.5 - 20.5i)T^{2}
43 1+(−2.42+1.40i)T+(21.5−37.2i)T2 1 + (-2.42 + 1.40i)T + (21.5 - 37.2i)T^{2}
47 1+(−3.04−0.816i)T+(40.7+23.5i)T2 1 + (-3.04 - 0.816i)T + (40.7 + 23.5i)T^{2}
53 1+(−3.66+6.34i)T+(−26.5−45.8i)T2 1 + (-3.66 + 6.34i)T + (-26.5 - 45.8i)T^{2}
59 1+(−2.93+2.93i)T−59iT2 1 + (-2.93 + 2.93i)T - 59iT^{2}
61 1+(−3.90−2.25i)T+(30.5+52.8i)T2 1 + (-3.90 - 2.25i)T + (30.5 + 52.8i)T^{2}
67 1+(−1.36−0.366i)T+(58.0+33.5i)T2 1 + (-1.36 - 0.366i)T + (58.0 + 33.5i)T^{2}
71 1+(−13.8−3.70i)T+(61.4+35.5i)T2 1 + (-13.8 - 3.70i)T + (61.4 + 35.5i)T^{2}
73 1+(−1.82−6.81i)T+(−63.2+36.5i)T2 1 + (-1.82 - 6.81i)T + (-63.2 + 36.5i)T^{2}
79 1+(−0.316−0.548i)T+(−39.5+68.4i)T2 1 + (-0.316 - 0.548i)T + (-39.5 + 68.4i)T^{2}
83 1+(−1.07−1.07i)T+83iT2 1 + (-1.07 - 1.07i)T + 83iT^{2}
89 1+(−9.60+9.60i)T−89iT2 1 + (-9.60 + 9.60i)T - 89iT^{2}
97 1+(−0.0487+0.181i)T+(−84.0−48.5i)T2 1 + (-0.0487 + 0.181i)T + (-84.0 - 48.5i)T^{2}
show more
show less
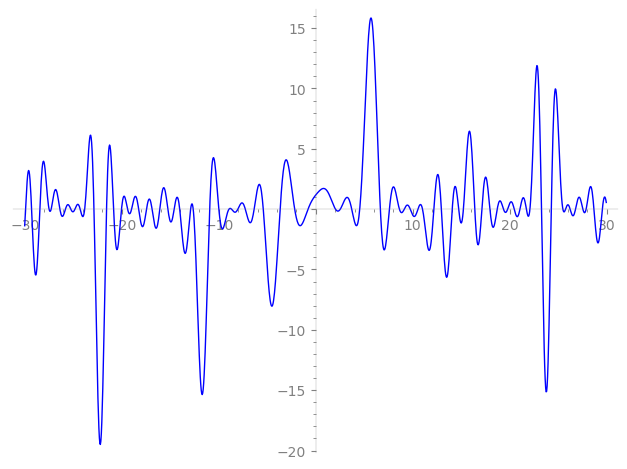
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.985922537179438384596310216768, −8.939903035050055453645097359060, −8.680603767934134280479755799879, −8.026458154849181949227685211052, −7.25835670485000188833687159479, −6.34730016209952083550394902778, −5.40737304091804598297012333972, −3.67050300587913366703867229306, −2.16831259424141905090545001325, −0.791930117588839082651286808422, 2.03722659257642604236417171096, 2.53324411341315071115373377573, 3.71221062940833013415930034045, 4.53504848999822076065552379161, 6.66240333631202600973021184473, 7.59509725203975571305421844126, 8.627411915901564087291878295008, 9.127810675323766776607779435260, 9.743102923131268584450295558440, 10.53843828027842234550071313236

Graph of the ZZ-function along the critical line