↑

Properties

Label 2-637-91.89-c1-0-19
Degree 22
Conductor 637637
Sign −0.777−0.628i-0.777 - 0.628i
Analytic cond. 5.086475.08647
Root an. cond. 2.255322.25532
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.67 + 1.67i)2-s + (1.04 + 0.601i)3-s + 3.60i·4-s + (0.825 + 3.08i)5-s + (0.736 + 2.74i)6-s + (−2.68 + 2.68i)8-s + (−0.777 − 1.34i)9-s + (−3.77 + 6.54i)10-s + (−1.10 − 4.11i)11-s + (−2.16 + 3.75i)12-s + (3.48 + 0.920i)13-s + (−0.992 + 3.70i)15-s − 1.79·16-s − 1.44·17-s + (0.952 − 3.55i)18-s + (−2.42 − 0.649i)19-s + ⋯
L(s)  = 1  + (1.18 + 1.18i)2-s + (0.601 + 0.347i)3-s + 1.80i·4-s + (0.369 + 1.37i)5-s + (0.300 + 1.12i)6-s + (−0.950 + 0.950i)8-s + (−0.259 − 0.448i)9-s + (−1.19 + 2.06i)10-s + (−0.332 − 1.23i)11-s + (−0.625 + 1.08i)12-s + (0.966 + 0.255i)13-s + (−0.256 + 0.956i)15-s − 0.448·16-s − 0.350·17-s + (0.224 − 0.838i)18-s + (−0.556 − 0.149i)19-s + ⋯

Functional equation

Λ(s)=(637s/2 ΓC(s) L(s)=((−0.777−0.628i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.777 - 0.628i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(637s/2 ΓC(s+1/2) L(s)=((−0.777−0.628i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.777 - 0.628i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 637637    =    72⋅137^{2} \cdot 13
Sign: −0.777−0.628i-0.777 - 0.628i
Analytic conductor: 5.086475.08647
Root analytic conductor: 2.255322.25532
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ637(362,⋅)\chi_{637} (362, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 637, ( :1/2), −0.777−0.628i)(2,\ 637,\ (\ :1/2),\ -0.777 - 0.628i)

Particular Values

L(1)L(1) ≈\approx 1.13354+3.20575i1.13354 + 3.20575i
L(12)L(\frac12) ≈\approx 1.13354+3.20575i1.13354 + 3.20575i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad7 1 1
13 1+(−3.48−0.920i)T 1 + (-3.48 - 0.920i)T
good2 1+(−1.67−1.67i)T+2iT2 1 + (-1.67 - 1.67i)T + 2iT^{2}
3 1+(−1.04−0.601i)T+(1.5+2.59i)T2 1 + (-1.04 - 0.601i)T + (1.5 + 2.59i)T^{2}
5 1+(−0.825−3.08i)T+(−4.33+2.5i)T2 1 + (-0.825 - 3.08i)T + (-4.33 + 2.5i)T^{2}
11 1+(1.10+4.11i)T+(−9.52+5.5i)T2 1 + (1.10 + 4.11i)T + (-9.52 + 5.5i)T^{2}
17 1+1.44T+17T2 1 + 1.44T + 17T^{2}
19 1+(2.42+0.649i)T+(16.4+9.5i)T2 1 + (2.42 + 0.649i)T + (16.4 + 9.5i)T^{2}
23 1+5.23iT−23T2 1 + 5.23iT - 23T^{2}
29 1+(−1.34−2.32i)T+(−14.5+25.1i)T2 1 + (-1.34 - 2.32i)T + (-14.5 + 25.1i)T^{2}
31 1+(−5.14−1.37i)T+(26.8+15.5i)T2 1 + (-5.14 - 1.37i)T + (26.8 + 15.5i)T^{2}
37 1+(−0.438+0.438i)T−37iT2 1 + (-0.438 + 0.438i)T - 37iT^{2}
41 1+(5.04+1.35i)T+(35.5+20.5i)T2 1 + (5.04 + 1.35i)T + (35.5 + 20.5i)T^{2}
43 1+(5.46+3.15i)T+(21.5+37.2i)T2 1 + (5.46 + 3.15i)T + (21.5 + 37.2i)T^{2}
47 1+(6.39−1.71i)T+(40.7−23.5i)T2 1 + (6.39 - 1.71i)T + (40.7 - 23.5i)T^{2}
53 1+(−3.79−6.56i)T+(−26.5+45.8i)T2 1 + (-3.79 - 6.56i)T + (-26.5 + 45.8i)T^{2}
59 1+(−1.43−1.43i)T+59iT2 1 + (-1.43 - 1.43i)T + 59iT^{2}
61 1+(4.53−2.62i)T+(30.5−52.8i)T2 1 + (4.53 - 2.62i)T + (30.5 - 52.8i)T^{2}
67 1+(8.46−2.26i)T+(58.0−33.5i)T2 1 + (8.46 - 2.26i)T + (58.0 - 33.5i)T^{2}
71 1+(−8.31+2.22i)T+(61.4−35.5i)T2 1 + (-8.31 + 2.22i)T + (61.4 - 35.5i)T^{2}
73 1+(4.09−15.2i)T+(−63.2−36.5i)T2 1 + (4.09 - 15.2i)T + (-63.2 - 36.5i)T^{2}
79 1+(1.00−1.74i)T+(−39.5−68.4i)T2 1 + (1.00 - 1.74i)T + (-39.5 - 68.4i)T^{2}
83 1+(−5.11+5.11i)T−83iT2 1 + (-5.11 + 5.11i)T - 83iT^{2}
89 1+(4.95+4.95i)T+89iT2 1 + (4.95 + 4.95i)T + 89iT^{2}
97 1+(−1.62−6.06i)T+(−84.0+48.5i)T2 1 + (-1.62 - 6.06i)T + (-84.0 + 48.5i)T^{2}
show more
show less
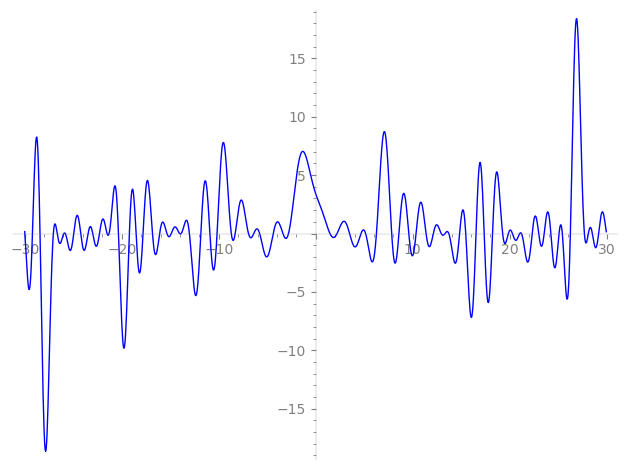
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.90762155873998999478750997754, −10.17017302395552789493905483039, −8.701480806329887688734173626333, −8.299662812750412598604565697834, −6.93085107540990682914089266429, −6.38784300828902565507073484586, −5.78105019567286752367410025140, −4.38324528439306708866916825579, −3.38527485909778066848201171643, −2.80683934906923212799248745898, 1.46356168347712078315503424466, 2.19886902641182525536732185422, 3.48754203456050373539790278626, 4.66856476623584455174871816698, 5.14221267529886539869554370342, 6.25905407321179438186127109982, 7.83109796115194892503155900402, 8.578148630712753109303378955344, 9.594665504351626240022524776687, 10.34343502469158653719182845908

Graph of the ZZ-function along the critical line