↑

Properties

Label 2-637-91.54-c1-0-17
Degree 22
Conductor 637637
Sign −0.451+0.892i-0.451 + 0.892i
Analytic cond. 5.086475.08647
Root an. cond. 2.255322.25532
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.0825 − 0.0825i)2-s + (−2.25 − 1.29i)3-s + 1.98i·4-s + (−1.70 + 0.456i)5-s + (−0.293 + 0.0785i)6-s + (0.329 + 0.329i)8-s + (1.87 + 3.25i)9-s + (−0.103 + 0.178i)10-s + (1.89 − 0.506i)11-s + (2.58 − 4.47i)12-s + (1.85 + 3.09i)13-s + (4.43 + 1.18i)15-s − 3.91·16-s − 4.27·17-s + (0.423 + 0.113i)18-s + (1.10 − 4.12i)19-s + ⋯
L(s)  = 1  + (0.0583 − 0.0583i)2-s + (−1.29 − 0.750i)3-s + 0.993i·4-s + (−0.762 + 0.204i)5-s + (−0.119 + 0.0320i)6-s + (0.116 + 0.116i)8-s + (0.625 + 1.08i)9-s + (−0.0325 + 0.0564i)10-s + (0.570 − 0.152i)11-s + (0.745 − 1.29i)12-s + (0.515 + 0.857i)13-s + (1.14 + 0.306i)15-s − 0.979·16-s − 1.03·17-s + (0.0997 + 0.0267i)18-s + (0.253 − 0.945i)19-s + ⋯

Functional equation

Λ(s)=(637s/2 ΓC(s) L(s)=((−0.451+0.892i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.451 + 0.892i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(637s/2 ΓC(s+1/2) L(s)=((−0.451+0.892i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 637 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.451 + 0.892i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 637637    =    72⋅137^{2} \cdot 13
Sign: −0.451+0.892i-0.451 + 0.892i
Analytic conductor: 5.086475.08647
Root analytic conductor: 2.255322.25532
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ637(509,⋅)\chi_{637} (509, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 637, ( :1/2), −0.451+0.892i)(2,\ 637,\ (\ :1/2),\ -0.451 + 0.892i)

Particular Values

L(1)L(1) ≈\approx 0.204244−0.332237i0.204244 - 0.332237i
L(12)L(\frac12) ≈\approx 0.204244−0.332237i0.204244 - 0.332237i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad7 1 1
13 1+(−1.85−3.09i)T 1 + (-1.85 - 3.09i)T
good2 1+(−0.0825+0.0825i)T−2iT2 1 + (-0.0825 + 0.0825i)T - 2iT^{2}
3 1+(2.25+1.29i)T+(1.5+2.59i)T2 1 + (2.25 + 1.29i)T + (1.5 + 2.59i)T^{2}
5 1+(1.70−0.456i)T+(4.33−2.5i)T2 1 + (1.70 - 0.456i)T + (4.33 - 2.5i)T^{2}
11 1+(−1.89+0.506i)T+(9.52−5.5i)T2 1 + (-1.89 + 0.506i)T + (9.52 - 5.5i)T^{2}
17 1+4.27T+17T2 1 + 4.27T + 17T^{2}
19 1+(−1.10+4.12i)T+(−16.4−9.5i)T2 1 + (-1.10 + 4.12i)T + (-16.4 - 9.5i)T^{2}
23 1+6.39iT−23T2 1 + 6.39iT - 23T^{2}
29 1+(3.57+6.19i)T+(−14.5+25.1i)T2 1 + (3.57 + 6.19i)T + (-14.5 + 25.1i)T^{2}
31 1+(−1.10+4.13i)T+(−26.8−15.5i)T2 1 + (-1.10 + 4.13i)T + (-26.8 - 15.5i)T^{2}
37 1+(2.00+2.00i)T+37iT2 1 + (2.00 + 2.00i)T + 37iT^{2}
41 1+(−2.94+11.0i)T+(−35.5−20.5i)T2 1 + (-2.94 + 11.0i)T + (-35.5 - 20.5i)T^{2}
43 1+(1.55+0.896i)T+(21.5+37.2i)T2 1 + (1.55 + 0.896i)T + (21.5 + 37.2i)T^{2}
47 1+(−1.71−6.40i)T+(−40.7+23.5i)T2 1 + (-1.71 - 6.40i)T + (-40.7 + 23.5i)T^{2}
53 1+(2.13+3.70i)T+(−26.5+45.8i)T2 1 + (2.13 + 3.70i)T + (-26.5 + 45.8i)T^{2}
59 1+(−1.19+1.19i)T−59iT2 1 + (-1.19 + 1.19i)T - 59iT^{2}
61 1+(−2.66+1.54i)T+(30.5−52.8i)T2 1 + (-2.66 + 1.54i)T + (30.5 - 52.8i)T^{2}
67 1+(−0.00510−0.0190i)T+(−58.0+33.5i)T2 1 + (-0.00510 - 0.0190i)T + (-58.0 + 33.5i)T^{2}
71 1+(−1.23−4.59i)T+(−61.4+35.5i)T2 1 + (-1.23 - 4.59i)T + (-61.4 + 35.5i)T^{2}
73 1+(−0.954−0.255i)T+(63.2+36.5i)T2 1 + (-0.954 - 0.255i)T + (63.2 + 36.5i)T^{2}
79 1+(−2.96+5.14i)T+(−39.5−68.4i)T2 1 + (-2.96 + 5.14i)T + (-39.5 - 68.4i)T^{2}
83 1+(9.87+9.87i)T+83iT2 1 + (9.87 + 9.87i)T + 83iT^{2}
89 1+(5.68−5.68i)T−89iT2 1 + (5.68 - 5.68i)T - 89iT^{2}
97 1+(14.2−3.82i)T+(84.0−48.5i)T2 1 + (14.2 - 3.82i)T + (84.0 - 48.5i)T^{2}
show more
show less
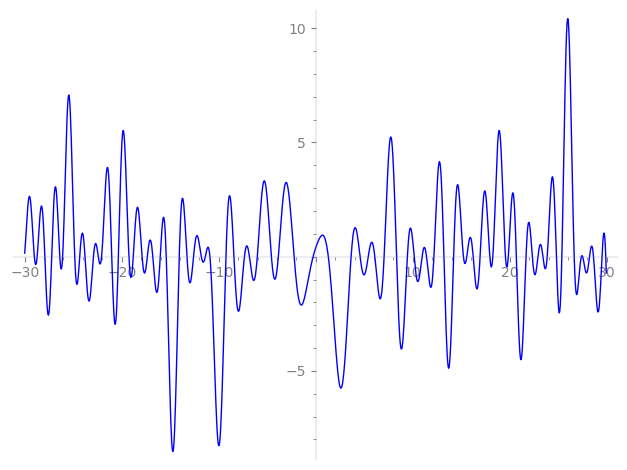
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.90479332367519476441647031550, −9.256933479145554993638506491570, −8.429424511511212521189682802605, −7.34800496496812920555209134679, −6.83398453642363304505605364565, −6.02246515085990435042817615505, −4.56873291885805171570181724707, −3.85315468450285957412962497633, −2.22882618532669364091370154725, −0.26963650482172148323046809431, 1.29825140219037848887732620286, 3.64596333818657275345147048770, 4.57665773711732733942581098342, 5.41437620965384616340465516102, 6.09242047140231035744516935942, 7.04926419149927532618378009806, 8.329132155619530814168342968958, 9.446624012125737354800206269729, 10.14863814427928669215826534270, 10.96134280338832096783120581021

Graph of the ZZ-function along the critical line