↑

Properties

Label 2-2e3-8.3-c14-0-10
Degree 22
Conductor 88
Sign −0.397+0.917i-0.397 + 0.917i
Analytic cond. 9.946319.94631
Root an. cond. 3.153773.15377
Motivic weight 1414
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (118. − 48.3i)2-s − 1.15e3·3-s + (1.17e4 − 1.14e4i)4-s + 9.66e3i·5-s + (−1.36e5 + 5.57e4i)6-s − 1.34e6i·7-s + (8.34e5 − 1.92e6i)8-s − 3.45e6·9-s + (4.67e5 + 1.14e6i)10-s − 8.97e5·11-s + (−1.35e7 + 1.32e7i)12-s − 5.37e7i·13-s + (−6.50e7 − 1.59e8i)14-s − 1.11e7i·15-s + (5.91e6 − 2.68e8i)16-s − 1.06e8·17-s + ⋯
L(s)  = 1  + (0.925 − 0.377i)2-s − 0.527·3-s + (0.714 − 0.699i)4-s + 0.123i·5-s + (−0.488 + 0.199i)6-s − 1.63i·7-s + (0.397 − 0.917i)8-s − 0.722·9-s + (0.0467 + 0.114i)10-s − 0.0460·11-s + (−0.376 + 0.368i)12-s − 0.857i·13-s + (−0.617 − 1.51i)14-s − 0.0652i·15-s + (0.0220 − 0.999i)16-s − 0.259·17-s + ⋯

Functional equation

Λ(s)=(8s/2 ΓC(s) L(s)=((−0.397+0.917i) Λ‾(15−s)\begin{aligned}\Lambda(s)=\mathstrut & 8 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.397 + 0.917i)\, \overline{\Lambda}(15-s) \end{aligned}
Λ(s)=(8s/2 ΓC(s+7) L(s)=((−0.397+0.917i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 8 ^{s/2} \, \Gamma_{\C}(s+7) \, L(s)\cr =\mathstrut & (-0.397 + 0.917i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 88    =    232^{3}
Sign: −0.397+0.917i-0.397 + 0.917i
Analytic conductor: 9.946319.94631
Root analytic conductor: 3.153773.15377
Motivic weight: 1414
Rational: no
Arithmetic: yes
Character: χ8(3,⋅)\chi_{8} (3, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 8, ( :7), −0.397+0.917i)(2,\ 8,\ (\ :7),\ -0.397 + 0.917i)

Particular Values

L(152)L(\frac{15}{2}) ≈\approx 1.20008−1.82856i1.20008 - 1.82856i
L(12)L(\frac12) ≈\approx 1.20008−1.82856i1.20008 - 1.82856i
L(8)L(8) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−118.+48.3i)T 1 + (-118. + 48.3i)T
good3 1+1.15e3T+4.78e6T2 1 + 1.15e3T + 4.78e6T^{2}
5 1−9.66e3iT−6.10e9T2 1 - 9.66e3iT - 6.10e9T^{2}
7 1+1.34e6iT−6.78e11T2 1 + 1.34e6iT - 6.78e11T^{2}
11 1+8.97e5T+3.79e14T2 1 + 8.97e5T + 3.79e14T^{2}
13 1+5.37e7iT−3.93e15T2 1 + 5.37e7iT - 3.93e15T^{2}
17 1+1.06e8T+1.68e17T2 1 + 1.06e8T + 1.68e17T^{2}
19 1−9.74e8T+7.99e17T2 1 - 9.74e8T + 7.99e17T^{2}
23 1−4.91e9iT−1.15e19T2 1 - 4.91e9iT - 1.15e19T^{2}
29 1−1.32e10iT−2.97e20T2 1 - 1.32e10iT - 2.97e20T^{2}
31 1−3.03e8iT−7.56e20T2 1 - 3.03e8iT - 7.56e20T^{2}
37 1+7.87e10iT−9.01e21T2 1 + 7.87e10iT - 9.01e21T^{2}
41 1+2.80e11T+3.79e22T2 1 + 2.80e11T + 3.79e22T^{2}
43 1−3.24e11T+7.38e22T2 1 - 3.24e11T + 7.38e22T^{2}
47 1+2.85e10iT−2.56e23T2 1 + 2.85e10iT - 2.56e23T^{2}
53 1+2.31e12iT−1.37e24T2 1 + 2.31e12iT - 1.37e24T^{2}
59 1−3.41e12T+6.19e24T2 1 - 3.41e12T + 6.19e24T^{2}
61 1−5.23e12iT−9.87e24T2 1 - 5.23e12iT - 9.87e24T^{2}
67 1−7.72e12T+3.67e25T2 1 - 7.72e12T + 3.67e25T^{2}
71 1−5.57e12iT−8.27e25T2 1 - 5.57e12iT - 8.27e25T^{2}
73 1+4.34e12T+1.22e26T2 1 + 4.34e12T + 1.22e26T^{2}
79 1+2.63e13iT−3.68e26T2 1 + 2.63e13iT - 3.68e26T^{2}
83 1+3.06e13T+7.36e26T2 1 + 3.06e13T + 7.36e26T^{2}
89 1−3.63e13T+1.95e27T2 1 - 3.63e13T + 1.95e27T^{2}
97 1−7.63e13T+6.52e27T2 1 - 7.63e13T + 6.52e27T^{2}
show more
show less
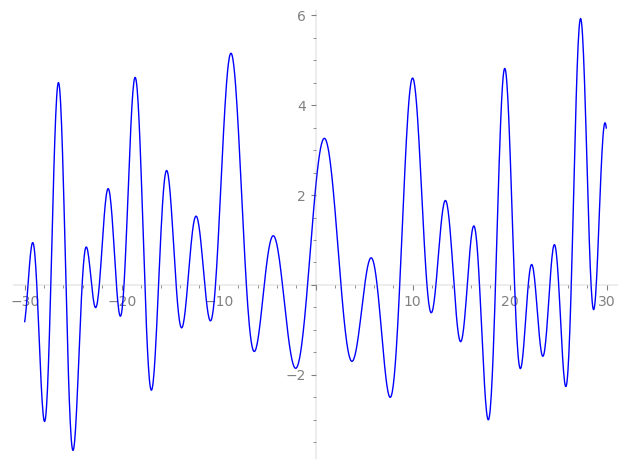
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−17.61004198531031113544821687864, −16.20005071241594507104192406045, −14.38739240479442914335663716542, −13.20485072906447241996961565804, −11.43382959858815767026710715588, −10.33178675497708328185770457691, −7.14809449477386439827619910232, −5.30459525712283686568098075219, −3.42678150360528532137602526213, −0.841414775344892205727968347331, 2.60343461002363547212616341344, 5.05241322465936846080236336931, 6.32500906862010424548057312458, 8.658661823672135355255472661365, 11.46636737583749215302669191003, 12.38854563739458707126510968958, 14.25894371617250801501947442881, 15.62360604749843609362959518916, 16.88232333497473952022432229268, 18.53079542247788088298427525239

Graph of the ZZ-function along the critical line