↑

Properties

Label 2-810-3.2-c2-0-13
Degree 22
Conductor 810810
Sign −i-i
Analytic cond. 22.070922.0709
Root an. cond. 4.697964.69796
Motivic weight 22
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

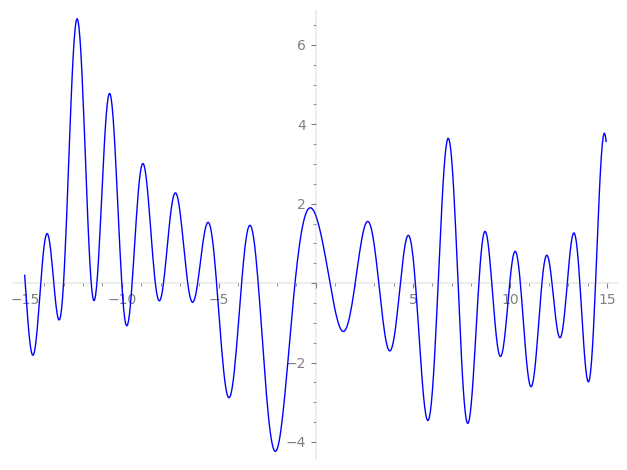
L(s)  = 1  + 1.41i·2-s − 2.00·4-s + 2.23i·5-s − 1.37·7-s − 2.82i·8-s − 3.16·10-s − 10.6i·11-s + 9.84·13-s − 1.94i·14-s + 4.00·16-s + 3.83i·17-s + 16.2·19-s − 4.47i·20-s + 14.9·22-s + 31.0i·23-s + ⋯
L(s)  = 1  + 0.707i·2-s − 0.500·4-s + 0.447i·5-s − 0.196·7-s − 0.353i·8-s − 0.316·10-s − 0.963i·11-s + 0.757·13-s − 0.138i·14-s + 0.250·16-s + 0.225i·17-s + 0.856·19-s − 0.223i·20-s + 0.681·22-s + 1.35i·23-s + ⋯

Functional equation

Λ(s)=(810s/2 ΓC(s) L(s)=(−i Λ‾(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 810 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -i\, \overline{\Lambda}(3-s) \end{aligned}
Λ(s)=(810s/2 ΓC(s+1) L(s)=(−i Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 810 ^{s/2} \, \Gamma_{\C}(s+1) \, L(s)\cr =\mathstrut & -i\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 810810    =    2⋅34⋅52 \cdot 3^{4} \cdot 5
Sign: −i-i
Analytic conductor: 22.070922.0709
Root analytic conductor: 4.697964.69796
Motivic weight: 22
Rational: no
Arithmetic: yes
Character: χ810(161,⋅)\chi_{810} (161, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 810, ( :1), −i)(2,\ 810,\ (\ :1),\ -i)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 1.6959835731.695983573
L(12)L(\frac12) ≈\approx 1.6959835731.695983573
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1−1.41iT 1 - 1.41iT
3 1 1
5 1−2.23iT 1 - 2.23iT
good7 1+1.37T+49T2 1 + 1.37T + 49T^{2}
11 1+10.6iT−121T2 1 + 10.6iT - 121T^{2}
13 1−9.84T+169T2 1 - 9.84T + 169T^{2}
17 1−3.83iT−289T2 1 - 3.83iT - 289T^{2}
19 1−16.2T+361T2 1 - 16.2T + 361T^{2}
23 1−31.0iT−529T2 1 - 31.0iT - 529T^{2}
29 1+19.6iT−841T2 1 + 19.6iT - 841T^{2}
31 1−43.8T+961T2 1 - 43.8T + 961T^{2}
37 1−35.1T+1.36e3T2 1 - 35.1T + 1.36e3T^{2}
41 1−71.1iT−1.68e3T2 1 - 71.1iT - 1.68e3T^{2}
43 1+43.8T+1.84e3T2 1 + 43.8T + 1.84e3T^{2}
47 1−72.9iT−2.20e3T2 1 - 72.9iT - 2.20e3T^{2}
53 1+62.2iT−2.80e3T2 1 + 62.2iT - 2.80e3T^{2}
59 1+29.8iT−3.48e3T2 1 + 29.8iT - 3.48e3T^{2}
61 1−108.T+3.72e3T2 1 - 108.T + 3.72e3T^{2}
67 1+65.0T+4.48e3T2 1 + 65.0T + 4.48e3T^{2}
71 1−90.6iT−5.04e3T2 1 - 90.6iT - 5.04e3T^{2}
73 1−71.2T+5.32e3T2 1 - 71.2T + 5.32e3T^{2}
79 1−14.4T+6.24e3T2 1 - 14.4T + 6.24e3T^{2}
83 1−134.iT−6.88e3T2 1 - 134. iT - 6.88e3T^{2}
89 1−102.iT−7.92e3T2 1 - 102. iT - 7.92e3T^{2}
97 1−159.T+9.40e3T2 1 - 159.T + 9.40e3T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.999353365731592035114468203520, −9.466348867195349471555869571711, −8.270741295896152019375325449959, −7.85073446532934751305755253294, −6.60138142359804482045796361707, −6.09087914645179746413168756976, −5.11523200692666409645586721759, −3.82748754199139512118378361930, −2.97260873853415694002325496722, −1.07641360370895090022098877124, 0.72727677592140340830011173661, 2.02435220502083696070657925213, 3.23952868352852307015344614488, 4.35186101289700997174545395808, 5.12375123681032759131625141310, 6.29771455681706046909034578517, 7.32244114601128638000420165610, 8.394338805092816030714514256899, 9.060465761080100343148046339260, 9.984227662331636155269457179444

Graph of the ZZ-function along the critical line