↑

Properties

Label 6-8112e3-1.1-c1e3-0-8
Degree 66
Conductor 533806460928533806460928
Sign −1-1
Analytic cond. 271778.271778.
Root an. cond. 8.048268.04826
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 33

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

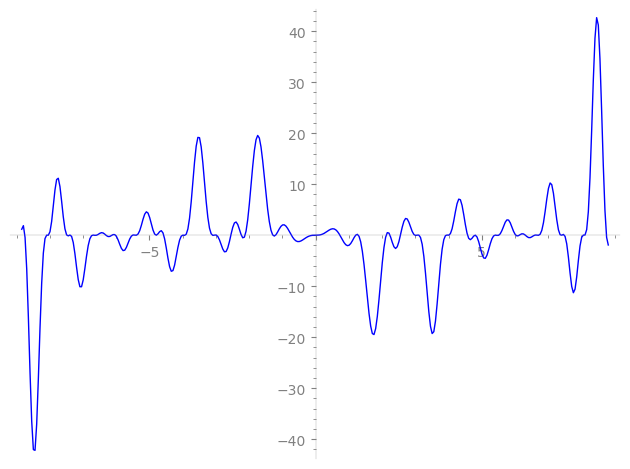
L(s)  = 1  − 3·3-s − 6·7-s + 6·9-s − 7·11-s + 3·17-s − 13·19-s + 18·21-s + 14·23-s − 8·25-s − 10·27-s + 10·29-s − 6·31-s + 21·33-s + 6·37-s + 13·41-s + 5·43-s − 7·47-s + 10·49-s − 9·51-s − 3·53-s + 39·57-s + 6·59-s − 61-s − 36·63-s − 33·67-s − 42·69-s + 6·71-s + ⋯
L(s)  = 1  − 1.73·3-s − 2.26·7-s + 2·9-s − 2.11·11-s + 0.727·17-s − 2.98·19-s + 3.92·21-s + 2.91·23-s − 8/5·25-s − 1.92·27-s + 1.85·29-s − 1.07·31-s + 3.65·33-s + 0.986·37-s + 2.03·41-s + 0.762·43-s − 1.02·47-s + 10/7·49-s − 1.26·51-s − 0.412·53-s + 5.16·57-s + 0.781·59-s − 0.128·61-s − 4.53·63-s − 4.03·67-s − 5.05·69-s + 0.712·71-s + ⋯

Functional equation

Λ(s)=((212⋅33⋅136)s/2 ΓC(s)3 L(s)=(− Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{3} \cdot 13^{6}\right)^{s/2} \, \Gamma_{\C}(s)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(2-s)\end{aligned}
Λ(s)=((212⋅33⋅136)s/2 ΓC(s+1/2)3 L(s)=(− Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{12} \cdot 3^{3} \cdot 13^{6}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{3} \, L(s)\cr=\mathstrut & -\,\Lambda(1-s)\end{aligned}

Invariants

Degree: 66
Conductor: 212⋅33⋅1362^{12} \cdot 3^{3} \cdot 13^{6}
Sign: −1-1
Analytic conductor: 271778.271778.
Root analytic conductor: 8.048268.04826
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 33
Selberg data: (6, 212⋅33⋅136, ( :1/2,1/2,1/2), −1)(6,\ 2^{12} \cdot 3^{3} \cdot 13^{6} ,\ ( \ : 1/2, 1/2, 1/2 ),\ -1 )

Particular Values

L(1)L(1) == 00
L(12)L(\frac12) == 00
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
3C1C_1 (1+T)3 ( 1 + T )^{3}
13 1 1
good5A4×C2A_4\times C_2 1+8T2+7T3+8pT4+p3T6 1 + 8 T^{2} + 7 T^{3} + 8 p T^{4} + p^{3} T^{6}
7A4×C2A_4\times C_2 1+6T+26T2+85T3+26pT4+6p2T5+p3T6 1 + 6 T + 26 T^{2} + 85 T^{3} + 26 p T^{4} + 6 p^{2} T^{5} + p^{3} T^{6}
11A4×C2A_4\times C_2 1+7T+47T2+161T3+47pT4+7p2T5+p3T6 1 + 7 T + 47 T^{2} + 161 T^{3} + 47 p T^{4} + 7 p^{2} T^{5} + p^{3} T^{6}
17A4×C2A_4\times C_2 1−3T+47T2−103T3+47pT4−3p2T5+p3T6 1 - 3 T + 47 T^{2} - 103 T^{3} + 47 p T^{4} - 3 p^{2} T^{5} + p^{3} T^{6}
19A4×C2A_4\times C_2 1+13T+97T2+481T3+97pT4+13p2T5+p3T6 1 + 13 T + 97 T^{2} + 481 T^{3} + 97 p T^{4} + 13 p^{2} T^{5} + p^{3} T^{6}
23A4×C2A_4\times C_2 1−14T+118T2−651T3+118pT4−14p2T5+p3T6 1 - 14 T + 118 T^{2} - 651 T^{3} + 118 p T^{4} - 14 p^{2} T^{5} + p^{3} T^{6}
29A4×C2A_4\times C_2 1−10T+90T2−567T3+90pT4−10p2T5+p3T6 1 - 10 T + 90 T^{2} - 567 T^{3} + 90 p T^{4} - 10 p^{2} T^{5} + p^{3} T^{6}
31A4×C2A_4\times C_2 1+6T+56T2+191T3+56pT4+6p2T5+p3T6 1 + 6 T + 56 T^{2} + 191 T^{3} + 56 p T^{4} + 6 p^{2} T^{5} + p^{3} T^{6}
37A4×C2A_4\times C_2 1−6T+2pT2−445T3+2p2T4−6p2T5+p3T6 1 - 6 T + 2 p T^{2} - 445 T^{3} + 2 p^{2} T^{4} - 6 p^{2} T^{5} + p^{3} T^{6}
41A4×C2A_4\times C_2 1−13T+149T2−983T3+149pT4−13p2T5+p3T6 1 - 13 T + 149 T^{2} - 983 T^{3} + 149 p T^{4} - 13 p^{2} T^{5} + p^{3} T^{6}
43A4×C2A_4\times C_2 1−5T+100T2−389T3+100pT4−5p2T5+p3T6 1 - 5 T + 100 T^{2} - 389 T^{3} + 100 p T^{4} - 5 p^{2} T^{5} + p^{3} T^{6}
47A4×C2A_4\times C_2 1+7T+85T2+357T3+85pT4+7p2T5+p3T6 1 + 7 T + 85 T^{2} + 357 T^{3} + 85 p T^{4} + 7 p^{2} T^{5} + p^{3} T^{6}
53A4×C2A_4\times C_2 1+3T+15T2−325T3+15pT4+3p2T5+p3T6 1 + 3 T + 15 T^{2} - 325 T^{3} + 15 p T^{4} + 3 p^{2} T^{5} + p^{3} T^{6}
59A4×C2A_4\times C_2 1−6T−7T2+404T3−7pT4−6p2T5+p3T6 1 - 6 T - 7 T^{2} + 404 T^{3} - 7 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6}
61A4×C2A_4\times C_2 1+T+111T2+163T3+111pT4+p2T5+p3T6 1 + T + 111 T^{2} + 163 T^{3} + 111 p T^{4} + p^{2} T^{5} + p^{3} T^{6}
67A4×C2A_4\times C_2 1+33T+557T2+5669T3+557pT4+33p2T5+p3T6 1 + 33 T + 557 T^{2} + 5669 T^{3} + 557 p T^{4} + 33 p^{2} T^{5} + p^{3} T^{6}
71A4×C2A_4\times C_2 1−6T+162T2−13pT3+162pT4−6p2T5+p3T6 1 - 6 T + 162 T^{2} - 13 p T^{3} + 162 p T^{4} - 6 p^{2} T^{5} + p^{3} T^{6}
73A4×C2A_4\times C_2 1−14T+212T2−1953T3+212pT4−14p2T5+p3T6 1 - 14 T + 212 T^{2} - 1953 T^{3} + 212 p T^{4} - 14 p^{2} T^{5} + p^{3} T^{6}
79A4×C2A_4\times C_2 1−11T+261T2−1751T3+261pT4−11p2T5+p3T6 1 - 11 T + 261 T^{2} - 1751 T^{3} + 261 p T^{4} - 11 p^{2} T^{5} + p^{3} T^{6}
83A4×C2A_4\times C_2 1+8T+100T2+1299T3+100pT4+8p2T5+p3T6 1 + 8 T + 100 T^{2} + 1299 T^{3} + 100 p T^{4} + 8 p^{2} T^{5} + p^{3} T^{6}
89A4×C2A_4\times C_2 1+7T+141T2+273T3+141pT4+7p2T5+p3T6 1 + 7 T + 141 T^{2} + 273 T^{3} + 141 p T^{4} + 7 p^{2} T^{5} + p^{3} T^{6}
97A4×C2A_4\times C_2 1−19T+346T2−3715T3+346pT4−19p2T5+p3T6 1 - 19 T + 346 T^{2} - 3715 T^{3} + 346 p T^{4} - 19 p^{2} T^{5} + p^{3} T^{6}
show more
show less
   L(s)=∏p ∏j=16(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{6} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−7.37022011004766787251642949141, −6.71981194587918788290424786158, −6.66975396196763504237313383110, −6.59077038303723228623100234776, −6.31025218374087677389105812764, −6.12844539490820135952952803904, −6.02188160081052329649926915263, −5.51250952524918086137506144380, −5.42934869667619169002760799221, −5.39023774707767006831233026496, −4.80648460225367436928455319423, −4.79308798146421432793064241491, −4.57118795956099656753855827238, −4.00674054661538619436325918595, −3.98038570135656662648328815725, −3.92167384996497426746763322221, −3.11019345331780987540545319888, −3.05080134041651731827755956288, −2.98094012196096485790552932787, −2.55131771279509385537543670759, −2.23632890725472614767458600096, −2.12191129076108914383486919264, −1.28705818829591757926300790777, −1.20508496717562071007319007153, −0.72925221299194677698636624754, 0, 0, 0, 0.72925221299194677698636624754, 1.20508496717562071007319007153, 1.28705818829591757926300790777, 2.12191129076108914383486919264, 2.23632890725472614767458600096, 2.55131771279509385537543670759, 2.98094012196096485790552932787, 3.05080134041651731827755956288, 3.11019345331780987540545319888, 3.92167384996497426746763322221, 3.98038570135656662648328815725, 4.00674054661538619436325918595, 4.57118795956099656753855827238, 4.79308798146421432793064241491, 4.80648460225367436928455319423, 5.39023774707767006831233026496, 5.42934869667619169002760799221, 5.51250952524918086137506144380, 6.02188160081052329649926915263, 6.12844539490820135952952803904, 6.31025218374087677389105812764, 6.59077038303723228623100234776, 6.66975396196763504237313383110, 6.71981194587918788290424786158, 7.37022011004766787251642949141

Graph of the ZZ-function along the critical line