↑

Properties

Label 1-3040-3040.1603-r0-0-0
Degree $1$
Conductor $3040$
Sign $0.339 - 0.940i$
Analytic cond. $14.1177$
Root an. cond. $14.1177$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.258 + 0.965i)3-s + 7-s + (−0.866 + 0.5i)9-s + (−0.707 + 0.707i)11-s + (−0.965 − 0.258i)13-s + (−0.866 − 0.5i)17-s + (0.258 + 0.965i)21-s + (−0.5 − 0.866i)23-s + (−0.707 − 0.707i)27-s + (−0.258 + 0.965i)29-s − 31-s + (−0.866 − 0.5i)33-s + (0.707 + 0.707i)37-s − i·39-s + (−0.866 − 0.5i)41-s + ⋯
L(s)  = 1  + (0.258 + 0.965i)3-s + 7-s + (−0.866 + 0.5i)9-s + (−0.707 + 0.707i)11-s + (−0.965 − 0.258i)13-s + (−0.866 − 0.5i)17-s + (0.258 + 0.965i)21-s + (−0.5 − 0.866i)23-s + (−0.707 − 0.707i)27-s + (−0.258 + 0.965i)29-s − 31-s + (−0.866 − 0.5i)33-s + (0.707 + 0.707i)37-s − i·39-s + (−0.866 − 0.5i)41-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3040 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.339 - 0.940i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3040 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.339 - 0.940i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(3040\)    =    \(2^{5} \cdot 5 \cdot 19\)
Sign: $0.339 - 0.940i$
Analytic conductor: \(14.1177\)
Root analytic conductor: \(14.1177\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3040} (1603, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 3040,\ (0:\ ),\ 0.339 - 0.940i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.5206312864 - 0.3656551643i\)
\(L(\frac12)\) \(\approx\) \(0.5206312864 - 0.3656551643i\)
\(L(1)\) \(\approx\) \(0.8972323883 + 0.2379339021i\)
\(L(1)\) \(\approx\) \(0.8972323883 + 0.2379339021i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
5 \( 1 \)
19 \( 1 \)
good3 \( 1 + (0.258 + 0.965i)T \)
7 \( 1 + T \)
11 \( 1 + (-0.707 + 0.707i)T \)
13 \( 1 + (-0.965 - 0.258i)T \)
17 \( 1 + (-0.866 - 0.5i)T \)
23 \( 1 + (-0.5 - 0.866i)T \)
29 \( 1 + (-0.258 + 0.965i)T \)
31 \( 1 - T \)
37 \( 1 + (0.707 + 0.707i)T \)
41 \( 1 + (-0.866 - 0.5i)T \)
43 \( 1 + (0.965 - 0.258i)T \)
47 \( 1 + (-0.866 + 0.5i)T \)
53 \( 1 + (0.258 - 0.965i)T \)
59 \( 1 + (-0.258 - 0.965i)T \)
61 \( 1 + (0.258 - 0.965i)T \)
67 \( 1 + (0.965 + 0.258i)T \)
71 \( 1 + (-0.866 - 0.5i)T \)
73 \( 1 + (0.5 - 0.866i)T \)
79 \( 1 + (0.5 - 0.866i)T \)
83 \( 1 + (-0.707 + 0.707i)T \)
89 \( 1 + (0.866 - 0.5i)T \)
97 \( 1 + (0.866 + 0.5i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

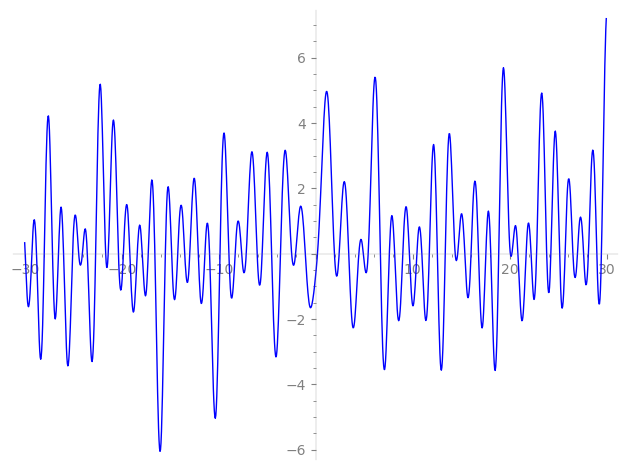
Imaginary part of the first few zeros on the critical line

−19.16241809913690505143879986265, −18.402480352131280912762862744972, −17.881671730651833156812224280276, −17.26297435327815559230908731352, −16.58032696230903654728601786598, −15.50486192164053998397517065044, −14.853176387867043233527137230190, −14.22564342059575647270358642751, −13.504973559021119744669308133536, −12.98199132789938675464489480913, −12.107929335585584697433247171123, −11.42211830678607323338914591558, −10.9420773414180795470585845822, −9.869797136301069146145578769, −8.95683834717213647935892005112, −8.30646619757575633207149356173, −7.633583960184287843032565241786, −7.162268694884283062008758540408, −6.03668350055943569997160785186, −5.52163750365518344821702755153, −4.54978046302637657476002817224, −3.63781793718226064977236279095, −2.48124484396294867083388948631, −2.07657834972848243069741233527, −1.0746813537308968279411867846, 0.18137367803221059009588473625, 1.9270897306531035675326465035, 2.41595409652871788546476312517, 3.404480109324258684999602424415, 4.44327097960613524523791662575, 4.90846360943208005776683281135, 5.40746118770996434434946762497, 6.659845801220396281745275831817, 7.58574214251201929375111819299, 8.13651855282680709953677582958, 8.97230786690852187162210618960, 9.65307621932029251086638002818, 10.42790328989838027720105335769, 10.94083972400298876315405860957, 11.70670759002855669978973005818, 12.53975440083223720215611116250, 13.34762381730095770680165418102, 14.37665735850164936449399693994, 14.63629907758277934974236630721, 15.37005081070105645700279262139, 16.01049801487803763710984212846, 16.78142495757680166704734205776, 17.53324405414937795457311603819, 18.04706080828723796692529853077, 18.859780672912939855511895698105

Graph of the $Z$-function along the critical line