↑

Properties

Label 1-143-143.109-r0-0-0
Degree $1$
Conductor $143$
Sign $0.957 + 0.289i$
Analytic cond. $0.664089$
Root an. cond. $0.664089$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + i·2-s + 3-s − 4-s − i·5-s + i·6-s − i·7-s − i·8-s + 9-s + 10-s − 12-s + 14-s − i·15-s + 16-s + 17-s + i·18-s + i·19-s + ⋯
L(s)  = 1  + i·2-s + 3-s − 4-s − i·5-s + i·6-s − i·7-s − i·8-s + 9-s + 10-s − 12-s + 14-s − i·15-s + 16-s + 17-s + i·18-s + i·19-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 143 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.957 + 0.289i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 143 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (0.957 + 0.289i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(143\)    =    \(11 \cdot 13\)
Sign: $0.957 + 0.289i$
Analytic conductor: \(0.664089\)
Root analytic conductor: \(0.664089\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{143} (109, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 143,\ (0:\ ),\ 0.957 + 0.289i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.346805925 + 0.1994198552i\)
\(L(\frac12)\) \(\approx\) \(1.346805925 + 0.1994198552i\)
\(L(1)\) \(\approx\) \(1.258641824 + 0.2578622694i\)
\(L(1)\) \(\approx\) \(1.258641824 + 0.2578622694i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad11 \( 1 \)
13 \( 1 \)
good2 \( 1 \)
3 \( 1 + T \)
5 \( 1 + iT \)
7 \( 1 + T \)
17 \( 1 + iT \)
19 \( 1 - iT \)
23 \( 1 - iT \)
29 \( 1 + T \)
31 \( 1 + T \)
37 \( 1 \)
41 \( 1 - T \)
43 \( 1 \)
47 \( 1 + T \)
53 \( 1 - iT \)
59 \( 1 + T \)
61 \( 1 + T \)
67 \( 1 + iT \)
71 \( 1 + iT \)
73 \( 1 + iT \)
79 \( 1 - iT \)
83 \( 1 \)
89 \( 1 - T \)
97 \( 1 - iT \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

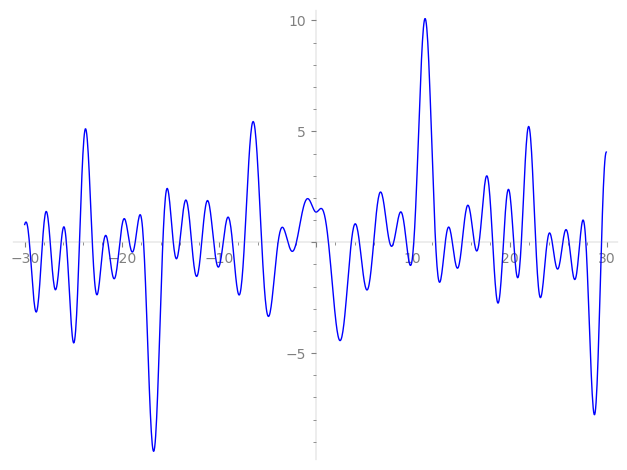
Imaginary part of the first few zeros on the critical line

−28.16549400790406089641513945318, −27.37102970789468360418788068494, −26.24020138640260851527912062714, −25.70539392596836969162759472809, −24.353270375809263249492422174126, −23.03001967850807613420195593503, −21.86527030567575588465633192701, −21.42777122515488642078797568691, −20.192459502316748997494280397885, −19.209487375541422627719730679583, −18.60771241545713260730512505506, −17.7475026724002339978638826385, −15.75899307621424045180797662702, −14.68395598549785445365728462994, −14.01622387828450638726706495356, −12.794039622823664800730306192, −11.75508572499933904760137322450, −10.51378756011140101897220819914, −9.53618723002762083502467689273, −8.57796918751578707860580631286, −7.34156714308083819189119634563, −5.57161013016443388615336441778, −3.87902836160945670415023845392, −2.86498193845507398310267851533, −1.99186038023159428592907653850, 1.31062539011728505162833747100, 3.668542538248435438768896918805, 4.50448068226851868919107209534, 5.9731654934656664092038071847, 7.61171678898497579936027621183, 8.035171073967760522780534466767, 9.344001748369312723108666721659, 10.10950762463439726717802937883, 12.35249971707495025725890204655, 13.35424203386018509007932263457, 14.07782767694350575220382056622, 15.09192732342894618968120916084, 16.34367173236884555452436517110, 16.84386914582941074151871804554, 18.24139903443520538475772632548, 19.352045842783011318586340065631, 20.40834257878928128884964620082, 21.19447921434604057823368220128, 22.6778939755487301599298400643, 23.85492691176050311050345783763, 24.37716381172935294676699169913, 25.47161864984576546876147188191, 26.11285655103608096317185561115, 27.222186602243917250920246905449, 27.84541691376297724874126409754

Graph of the $Z$-function along the critical line