↑

Properties

Label 1-143-143.137-r1-0-0
Degree $1$
Conductor $143$
Sign $0.289 - 0.957i$
Analytic cond. $15.3674$
Root an. cond. $15.3674$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.406 + 0.913i)2-s + (0.669 − 0.743i)3-s + (−0.669 − 0.743i)4-s + (0.587 − 0.809i)5-s + (0.406 + 0.913i)6-s + (0.743 − 0.669i)7-s + (0.951 − 0.309i)8-s + (−0.104 − 0.994i)9-s + (0.5 + 0.866i)10-s − 12-s + (0.309 + 0.951i)14-s + (−0.207 − 0.978i)15-s + (−0.104 + 0.994i)16-s + (−0.913 + 0.406i)17-s + (0.951 + 0.309i)18-s + (0.207 − 0.978i)19-s + ⋯
L(s)  = 1  + (−0.406 + 0.913i)2-s + (0.669 − 0.743i)3-s + (−0.669 − 0.743i)4-s + (0.587 − 0.809i)5-s + (0.406 + 0.913i)6-s + (0.743 − 0.669i)7-s + (0.951 − 0.309i)8-s + (−0.104 − 0.994i)9-s + (0.5 + 0.866i)10-s − 12-s + (0.309 + 0.951i)14-s + (−0.207 − 0.978i)15-s + (−0.104 + 0.994i)16-s + (−0.913 + 0.406i)17-s + (0.951 + 0.309i)18-s + (0.207 − 0.978i)19-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 143 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (0.289 - 0.957i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 143 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (0.289 - 0.957i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(143\)    =    \(11 \cdot 13\)
Sign: $0.289 - 0.957i$
Analytic conductor: \(15.3674\)
Root analytic conductor: \(15.3674\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{143} (137, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 143,\ (1:\ ),\ 0.289 - 0.957i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.489034510 - 1.104729436i\)
\(L(\frac12)\) \(\approx\) \(1.489034510 - 1.104729436i\)
\(L(1)\) \(\approx\) \(1.173620899 - 0.2456673188i\)
\(L(1)\) \(\approx\) \(1.173620899 - 0.2456673188i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad11 \( 1 \)
13 \( 1 \)
good2 \( 1 + (-0.406 + 0.913i)T \)
3 \( 1 + (0.669 - 0.743i)T \)
5 \( 1 + (0.587 - 0.809i)T \)
7 \( 1 + (0.743 - 0.669i)T \)
17 \( 1 + (-0.913 + 0.406i)T \)
19 \( 1 + (0.207 - 0.978i)T \)
23 \( 1 + (0.5 + 0.866i)T \)
29 \( 1 + (-0.978 + 0.207i)T \)
31 \( 1 + (-0.587 - 0.809i)T \)
37 \( 1 + (0.207 + 0.978i)T \)
41 \( 1 + (0.743 + 0.669i)T \)
43 \( 1 + (0.5 - 0.866i)T \)
47 \( 1 + (0.951 - 0.309i)T \)
53 \( 1 + (-0.809 + 0.587i)T \)
59 \( 1 + (0.743 - 0.669i)T \)
61 \( 1 + (0.913 - 0.406i)T \)
67 \( 1 + (0.866 - 0.5i)T \)
71 \( 1 + (0.406 + 0.913i)T \)
73 \( 1 + (-0.951 - 0.309i)T \)
79 \( 1 + (-0.809 + 0.587i)T \)
83 \( 1 + (0.587 - 0.809i)T \)
89 \( 1 + (-0.866 + 0.5i)T \)
97 \( 1 + (0.994 - 0.104i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

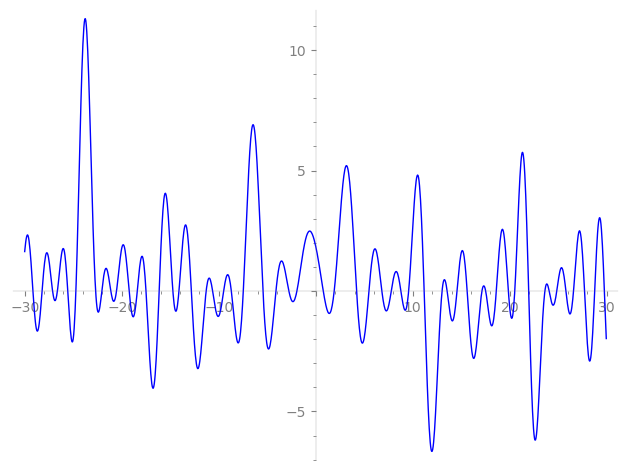
Imaginary part of the first few zeros on the critical line

−28.207081684834503290133017795287, −27.126239858329682414080513934080, −26.62787359110464049941131210193, −25.56194117979493559837814584550, −24.72302937198305687248611341284, −22.68747340823137910415704634053, −22.04680665777292596035209027687, −21.12093102097760898453559357181, −20.53511834170593621889332455181, −19.23258188518076373861842017771, −18.39501379714107060509592435923, −17.4957373156319082789910683493, −16.13878506220384324766002844870, −14.72487193783433901016421658302, −14.09811035334036084227680308517, −12.82052172000787654431146016818, −11.29388385342197252110940711154, −10.630249185421278319900492822281, −9.48912044936930932850712512494, −8.70057029142545193663043929914, −7.466379371687210581306178139024, −5.44065312227508532764078190010, −4.1002109482896685641984148300, −2.76770860743130764595770617898, −1.9399938416140803167806142451, 0.77677006441035665573504506812, 1.9042544415229415416365353689, 4.21157194159212596612792036257, 5.48513477291720974916444813923, 6.817295487955588273646006767409, 7.78687153521270370685617248139, 8.77913714541632613393761546687, 9.57885366883675462445643628215, 11.17571873634948670145534721984, 13.02458525778752509540778007563, 13.543482961689089755828022706666, 14.56201547734923097405938218968, 15.60956253287708138877851408871, 17.135368524263705687466042228838, 17.516215165156846003102158585921, 18.61322625663265377906519386085, 19.85654013633598205626167146678, 20.51776906766189015221427177460, 21.95079676465302667192245071113, 23.62263859998771767256948811910, 24.0618899337415540391464802183, 24.84662561356218945518482257077, 25.78876879430436636045722010142, 26.57413190380178907884967910472, 27.705702196727918967554860027895

Graph of the $Z$-function along the critical line