↑

Properties

Label 1-200-200.3-r0-0-0
Degree $1$
Conductor $200$
Sign $-0.535 + 0.844i$
Analytic cond. $0.928796$
Root an. cond. $0.928796$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.951 + 0.309i)3-s − i·7-s + (0.809 − 0.587i)9-s + (−0.809 − 0.587i)11-s + (0.587 + 0.809i)13-s + (−0.951 − 0.309i)17-s + (−0.309 + 0.951i)19-s + (−0.309 − 0.951i)21-s + (−0.587 + 0.809i)23-s + (−0.587 + 0.809i)27-s + (0.309 + 0.951i)29-s + (−0.309 + 0.951i)31-s + (0.951 + 0.309i)33-s + (−0.587 − 0.809i)37-s + (−0.809 − 0.587i)39-s + ⋯
L(s)  = 1  + (−0.951 + 0.309i)3-s − i·7-s + (0.809 − 0.587i)9-s + (−0.809 − 0.587i)11-s + (0.587 + 0.809i)13-s + (−0.951 − 0.309i)17-s + (−0.309 + 0.951i)19-s + (−0.309 − 0.951i)21-s + (−0.587 + 0.809i)23-s + (−0.587 + 0.809i)27-s + (0.309 + 0.951i)29-s + (−0.309 + 0.951i)31-s + (0.951 + 0.309i)33-s + (−0.587 − 0.809i)37-s + (−0.809 − 0.587i)39-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 200 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.535 + 0.844i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 200 ^{s/2} \, \Gamma_{\R}(s) \, L(s)\cr =\mathstrut & (-0.535 + 0.844i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(1\)
Conductor: \(200\)    =    \(2^{3} \cdot 5^{2}\)
Sign: $-0.535 + 0.844i$
Analytic conductor: \(0.928796\)
Root analytic conductor: \(0.928796\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{200} (3, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((1,\ 200,\ (0:\ ),\ -0.535 + 0.844i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.2736371921 + 0.4977442046i\)
\(L(\frac12)\) \(\approx\) \(0.2736371921 + 0.4977442046i\)
\(L(1)\) \(\approx\) \(0.6348273731 + 0.2427883576i\)
\(L(1)\) \(\approx\) \(0.6348273731 + 0.2427883576i\)

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
5 \( 1 \)
good3 \( 1 + (-0.951 + 0.309i)T \)
7 \( 1 - iT \)
11 \( 1 + (-0.809 - 0.587i)T \)
13 \( 1 + (0.587 + 0.809i)T \)
17 \( 1 + (-0.951 - 0.309i)T \)
19 \( 1 + (-0.309 + 0.951i)T \)
23 \( 1 + (-0.587 + 0.809i)T \)
29 \( 1 + (0.309 + 0.951i)T \)
31 \( 1 + (-0.309 + 0.951i)T \)
37 \( 1 + (-0.587 - 0.809i)T \)
41 \( 1 + (-0.809 + 0.587i)T \)
43 \( 1 + iT \)
47 \( 1 + (-0.951 + 0.309i)T \)
53 \( 1 + (0.951 - 0.309i)T \)
59 \( 1 + (0.809 - 0.587i)T \)
61 \( 1 + (0.809 + 0.587i)T \)
67 \( 1 + (-0.951 - 0.309i)T \)
71 \( 1 + (-0.309 - 0.951i)T \)
73 \( 1 + (0.587 - 0.809i)T \)
79 \( 1 + (0.309 + 0.951i)T \)
83 \( 1 + (0.951 + 0.309i)T \)
89 \( 1 + (0.809 + 0.587i)T \)
97 \( 1 + (0.951 - 0.309i)T \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ (1 - \alpha_{p}\, p^{-s})^{-1}\)

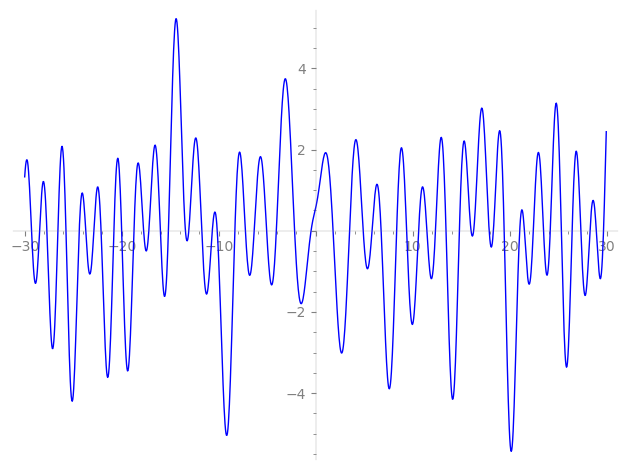
Imaginary part of the first few zeros on the critical line

−26.57761830965674449661441370819, −25.74369359865218948348348489465, −24.37913913773818130215215966317, −23.70509100498744900591390220544, −22.87121290779899380166009628323, −22.12754015394932319348922666802, −20.80816661388769053122250856843, −20.00332288235995144500754714064, −18.73853893207091299041504880736, −17.7405242142036787571914343579, −17.20284323095417001067093471076, −16.013596864777135202681543039, −15.18542306842532422590527125118, −13.42916856746294803756199608610, −13.08505048788713214039461574377, −11.74766324002514017239157462626, −10.66148189270874733899276812532, −10.15095431897031323610037113129, −8.33608436952742948545425502941, −7.24862552425086871583039428779, −6.34447372264862091572902872936, −5.05949758211529482372644394839, −4.05983410113788513272787845507, −2.17897379614529462617909654840, −0.48108368046527431566392026400, 1.78874638294315146385941756382, 3.48174431867222170946660562005, 4.893190964887223781508693277259, 5.803503988798860704150504073570, 6.74192696673321391780177836973, 8.3386215869800799182853315356, 9.36944738862950554579174417906, 10.603610416977542054993547511746, 11.460827543398259143184464612338, 12.34297709694154324886976961850, 13.43307794286949793219184981211, 14.80788992279846331046319307130, 16.01294580490254474812171517052, 16.27798990029838089765233598344, 17.879604653838630871607178078770, 18.31408714582767145100586525576, 19.42552065449808579392271934040, 21.025809971481356982169750566110, 21.512704934878231056255558880944, 22.42837521574886261922992895953, 23.48311238578441950553402236349, 24.1752712910537416998026975948, 25.31684479177583466617918906003, 26.42989172226968078956894030457, 27.3285530271797878155946541393

Graph of the $Z$-function along the critical line