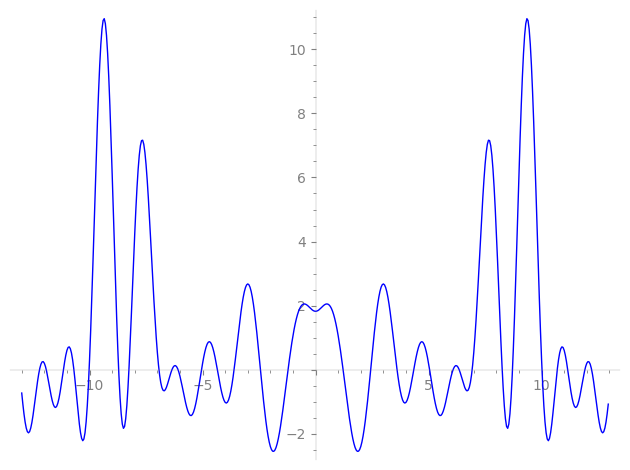
| L(s) = 1 | + 2-s − 3-s + 4-s − 6-s + 8-s + 11-s − 12-s + 13-s + 16-s − 2·19-s + 22-s − 24-s + 26-s + 27-s + 29-s + 31-s + 32-s − 33-s − 2·38-s − 39-s − 43-s + 44-s − 47-s − 48-s + 49-s + 52-s + 53-s + ⋯ |
| L(s) = 1 | + 2-s − 3-s + 4-s − 6-s + 8-s + 11-s − 12-s + 13-s + 16-s − 2·19-s + 22-s − 24-s + 26-s + 27-s + 29-s + 31-s + 32-s − 33-s − 2·38-s − 39-s − 43-s + 44-s − 47-s − 48-s + 49-s + 52-s + 53-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 2900 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2900 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(\frac{1}{2})\) |
\(\approx\) |
\(1.822108923\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.822108923\) |
| \(L(1)\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 - T \) |
| 5 | \( 1 \) |
| 29 | \( 1 - T \) |
| good | 3 | \( 1 + T + T^{2} \) |
| 7 | \( ( 1 - T )( 1 + T ) \) |
| 11 | \( 1 - T + T^{2} \) |
| 13 | \( 1 - T + T^{2} \) |
| 17 | \( ( 1 - T )( 1 + T ) \) |
| 19 | \( ( 1 + T )^{2} \) |
| 23 | \( ( 1 - T )( 1 + T ) \) |
| 31 | \( 1 - T + T^{2} \) |
| 37 | \( ( 1 - T )( 1 + T ) \) |
| 41 | \( ( 1 - T )( 1 + T ) \) |
| 43 | \( 1 + T + T^{2} \) |
| 47 | \( 1 + T + T^{2} \) |
| 53 | \( 1 - T + T^{2} \) |
| 59 | \( ( 1 - T )( 1 + T ) \) |
| 61 | \( ( 1 - T )( 1 + T ) \) |
| 67 | \( ( 1 - T )( 1 + T ) \) |
| 71 | \( ( 1 - T )( 1 + T ) \) |
| 73 | \( ( 1 - T )( 1 + T ) \) |
| 79 | \( 1 - T + T^{2} \) |
| 83 | \( ( 1 - T )( 1 + T ) \) |
| 89 | \( ( 1 - T )( 1 + T ) \) |
| 97 | \( ( 1 - T )( 1 + T ) \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.711804801139918925210406180077, −8.257322408471460048710337538077, −6.92824913823010019044738440566, −6.35281642484554886536638259247, −6.08452743621292393512593483271, −5.04507259923213383029497128817, −4.34497923838476092007487724748, −3.60524622122909792481413289148, −2.43869249622059524125528432624, −1.21726200800458325626463581473,
1.21726200800458325626463581473, 2.43869249622059524125528432624, 3.60524622122909792481413289148, 4.34497923838476092007487724748, 5.04507259923213383029497128817, 6.08452743621292393512593483271, 6.35281642484554886536638259247, 6.92824913823010019044738440566, 8.257322408471460048710337538077, 8.711804801139918925210406180077