↑

Properties

Label 2-11-11.10-c4-0-1
Degree 22
Conductor 1111
Sign 11
Analytic cond. 1.137061.13706
Root an. cond. 1.066331.06633
Motivic weight 44
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank 00

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

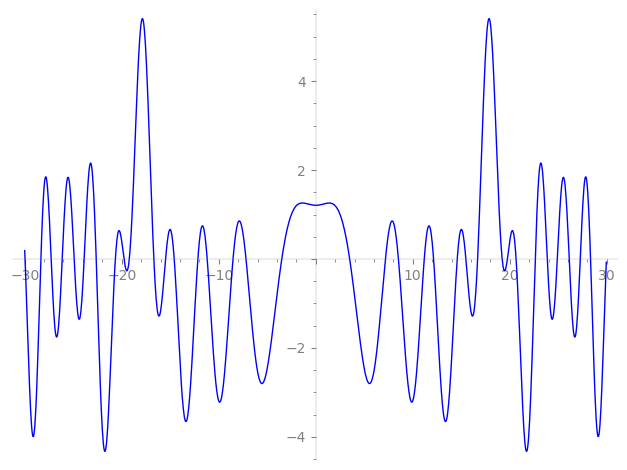
L(s)  = 1  + 7·3-s + 16·4-s − 49·5-s − 32·9-s + 121·11-s + 112·12-s − 343·15-s + 256·16-s − 784·20-s + 167·23-s + 1.77e3·25-s − 791·27-s − 553·31-s + 847·33-s − 512·36-s − 2.11e3·37-s + 1.93e3·44-s + 1.56e3·45-s − 1.91e3·47-s + 1.79e3·48-s + 2.40e3·49-s − 718·53-s − 5.92e3·55-s + 4.48e3·59-s − 5.48e3·60-s + 4.09e3·64-s − 7.75e3·67-s + ⋯
L(s)  = 1  + 7/9·3-s + 4-s − 1.95·5-s − 0.395·9-s + 11-s + 7/9·12-s − 1.52·15-s + 16-s − 1.95·20-s + 0.315·23-s + 2.84·25-s − 1.08·27-s − 0.575·31-s + 7/9·33-s − 0.395·36-s − 1.54·37-s + 44-s + 0.774·45-s − 0.868·47-s + 7/9·48-s + 49-s − 0.255·53-s − 1.95·55-s + 1.28·59-s − 1.52·60-s + 64-s − 1.72·67-s + ⋯

Functional equation

Λ(s)=(11s/2 ΓC(s) L(s)=( Λ(5−s)\begin{aligned}\Lambda(s)=\mathstrut & 11 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(5-s) \end{aligned}
Λ(s)=(11s/2 ΓC(s+2) L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 11 ^{s/2} \, \Gamma_{\C}(s+2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 1111
Sign: 11
Analytic conductor: 1.137061.13706
Root analytic conductor: 1.066331.06633
Motivic weight: 44
Rational: yes
Arithmetic: yes
Character: χ11(10,⋅)\chi_{11} (10, \cdot )
Primitive: yes
Self-dual: yes
Analytic rank: 00
Selberg data: (2, 11, ( :2), 1)(2,\ 11,\ (\ :2),\ 1)

Particular Values

L(52)L(\frac{5}{2}) ≈\approx 1.2066814871.206681487
L(12)L(\frac12) ≈\approx 1.2066814871.206681487
L(3)L(3) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad11 1−p2T 1 - p^{2} T
good2 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
3 1−7T+p4T2 1 - 7 T + p^{4} T^{2}
5 1+49T+p4T2 1 + 49 T + p^{4} T^{2}
7 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
13 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
17 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
19 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
23 1−167T+p4T2 1 - 167 T + p^{4} T^{2}
29 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
31 1+553T+p4T2 1 + 553 T + p^{4} T^{2}
37 1+2113T+p4T2 1 + 2113 T + p^{4} T^{2}
41 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
43 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
47 1+1918T+p4T2 1 + 1918 T + p^{4} T^{2}
53 1+718T+p4T2 1 + 718 T + p^{4} T^{2}
59 1−4487T+p4T2 1 - 4487 T + p^{4} T^{2}
61 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
67 1+7753T+p4T2 1 + 7753 T + p^{4} T^{2}
71 1−7607T+p4T2 1 - 7607 T + p^{4} T^{2}
73 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
79 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
83 (1−p2T)(1+p2T) ( 1 - p^{2} T )( 1 + p^{2} T )
89 1+6433T+p4T2 1 + 6433 T + p^{4} T^{2}
97 1+9793T+p4T2 1 + 9793 T + p^{4} T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−19.75885494398119872252381855677, −19.21831500864514360034759155597, −16.68606130447771987237201821798, −15.47741591826257693856979377606, −14.58729990820295578316234063201, −12.14791799560031264064261886161, −11.18632149482410471750487909209, −8.524438658210435446274777614942, −7.18620362855703168198936251634, −3.49864671127385759292183735940, 3.49864671127385759292183735940, 7.18620362855703168198936251634, 8.524438658210435446274777614942, 11.18632149482410471750487909209, 12.14791799560031264064261886161, 14.58729990820295578316234063201, 15.47741591826257693856979377606, 16.68606130447771987237201821798, 19.21831500864514360034759155597, 19.75885494398119872252381855677

Graph of the ZZ-function along the critical line