↑

Properties

Label 2-1260-1260.299-c0-0-3
Degree $2$
Conductor $1260$
Sign $-0.296 + 0.954i$
Analytic cond. $0.628821$
Root an. cond. $0.792982$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.866 − 0.5i)2-s + (0.866 − 0.5i)3-s + (0.499 − 0.866i)4-s − 5-s + (0.499 − 0.866i)6-s + (−0.866 − 0.5i)7-s − 0.999i·8-s + (0.499 − 0.866i)9-s + (−0.866 + 0.5i)10-s − 0.999i·12-s − 0.999·14-s + (−0.866 + 0.5i)15-s + (−0.5 − 0.866i)16-s − 0.999i·18-s + (−0.499 + 0.866i)20-s − 0.999·21-s + ⋯
L(s)  = 1  + (0.866 − 0.5i)2-s + (0.866 − 0.5i)3-s + (0.499 − 0.866i)4-s − 5-s + (0.499 − 0.866i)6-s + (−0.866 − 0.5i)7-s − 0.999i·8-s + (0.499 − 0.866i)9-s + (−0.866 + 0.5i)10-s − 0.999i·12-s − 0.999·14-s + (−0.866 + 0.5i)15-s + (−0.5 − 0.866i)16-s − 0.999i·18-s + (−0.499 + 0.866i)20-s − 0.999·21-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1260 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.296 + 0.954i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1260 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.296 + 0.954i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1260\)    =    \(2^{2} \cdot 3^{2} \cdot 5 \cdot 7\)
Sign: $-0.296 + 0.954i$
Analytic conductor: \(0.628821\)
Root analytic conductor: \(0.792982\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1260} (299, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1260,\ (\ :0),\ -0.296 + 0.954i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.804378035\)
\(L(\frac12)\) \(\approx\) \(1.804378035\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.866 + 0.5i)T \)
3 \( 1 + (-0.866 + 0.5i)T \)
5 \( 1 + T \)
7 \( 1 + (0.866 + 0.5i)T \)
good11 \( 1 + T^{2} \)
13 \( 1 + (-0.5 + 0.866i)T^{2} \)
17 \( 1 + (0.5 - 0.866i)T^{2} \)
19 \( 1 + (-0.5 - 0.866i)T^{2} \)
23 \( 1 - 2iT - T^{2} \)
29 \( 1 + (-1.5 - 0.866i)T + (0.5 + 0.866i)T^{2} \)
31 \( 1 + (-0.5 - 0.866i)T^{2} \)
37 \( 1 + (0.5 + 0.866i)T^{2} \)
41 \( 1 + (-0.5 - 0.866i)T + (-0.5 + 0.866i)T^{2} \)
43 \( 1 + (-0.866 + 1.5i)T + (-0.5 - 0.866i)T^{2} \)
47 \( 1 + (0.866 + 1.5i)T + (-0.5 + 0.866i)T^{2} \)
53 \( 1 + (-0.5 + 0.866i)T^{2} \)
59 \( 1 + (0.5 + 0.866i)T^{2} \)
61 \( 1 + (0.5 - 0.866i)T^{2} \)
67 \( 1 + (-0.5 - 0.866i)T^{2} \)
71 \( 1 + T^{2} \)
73 \( 1 + (-0.5 + 0.866i)T^{2} \)
79 \( 1 + (0.5 - 0.866i)T^{2} \)
83 \( 1 + (0.866 - 1.5i)T + (-0.5 - 0.866i)T^{2} \)
89 \( 1 + (1 - 1.73i)T + (-0.5 - 0.866i)T^{2} \)
97 \( 1 + (-0.5 - 0.866i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

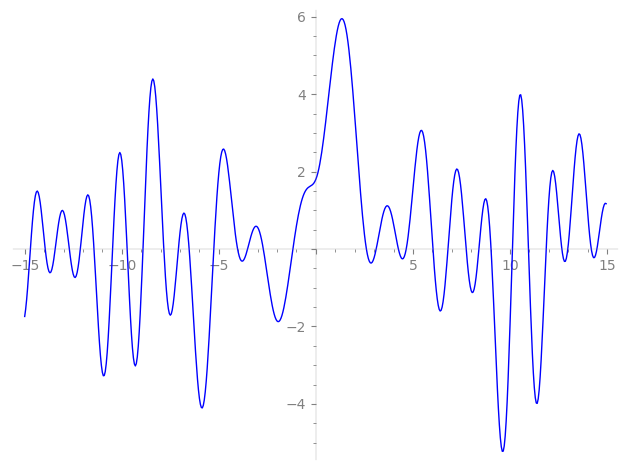
Imaginary part of the first few zeros on the critical line

−9.722903308503074943187783227164, −8.906306890734304115196595285779, −7.83402656602402720356312652080, −7.08306263283818787325872646738, −6.52896801410802086717922928816, −5.25932466250393343784622561448, −4.03295640683285972302453678291, −3.52041502107327942795861360787, −2.70895887295229795491606934733, −1.18522564287751680934537943335, 2.60121535867422162821335173420, 3.10502512536619287865005350163, 4.24942676342106737749656615011, 4.65159310679076219922108652710, 6.02831129149565488126926598592, 6.80200915222145220340710965467, 7.74017106697005777442533150196, 8.396080466477199243907773762826, 9.021106584700497471244897484133, 10.12138138219703362379779919558

Graph of the $Z$-function along the critical line