↑

Properties

Label 2-1332-444.119-c0-0-1
Degree $2$
Conductor $1332$
Sign $-0.232 + 0.972i$
Analytic cond. $0.664754$
Root an. cond. $0.815324$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.258 + 0.965i)2-s + (−0.866 − 0.499i)4-s + (−0.448 − 1.67i)5-s + (0.707 − 0.707i)8-s + 1.73·10-s + (−1.36 + 0.366i)13-s + (0.500 + 0.866i)16-s + (−1.67 − 0.448i)17-s + (−0.448 + 1.67i)20-s + (−1.73 + 1.00i)25-s − 1.41i·26-s + (−1.22 − 1.22i)29-s + (−0.965 + 0.258i)32-s + (0.866 − 1.50i)34-s + (0.866 + 0.5i)37-s + ⋯
L(s)  = 1  + (−0.258 + 0.965i)2-s + (−0.866 − 0.499i)4-s + (−0.448 − 1.67i)5-s + (0.707 − 0.707i)8-s + 1.73·10-s + (−1.36 + 0.366i)13-s + (0.500 + 0.866i)16-s + (−1.67 − 0.448i)17-s + (−0.448 + 1.67i)20-s + (−1.73 + 1.00i)25-s − 1.41i·26-s + (−1.22 − 1.22i)29-s + (−0.965 + 0.258i)32-s + (0.866 − 1.50i)34-s + (0.866 + 0.5i)37-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.232 + 0.972i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1332 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.232 + 0.972i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1332\)    =    \(2^{2} \cdot 3^{2} \cdot 37\)
Sign: $-0.232 + 0.972i$
Analytic conductor: \(0.664754\)
Root analytic conductor: \(0.815324\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1332} (1007, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1332,\ (\ :0),\ -0.232 + 0.972i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.3769364725\)
\(L(\frac12)\) \(\approx\) \(0.3769364725\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (0.258 - 0.965i)T \)
3 \( 1 \)
37 \( 1 + (-0.866 - 0.5i)T \)
good5 \( 1 + (0.448 + 1.67i)T + (-0.866 + 0.5i)T^{2} \)
7 \( 1 + (0.5 + 0.866i)T^{2} \)
11 \( 1 - T^{2} \)
13 \( 1 + (1.36 - 0.366i)T + (0.866 - 0.5i)T^{2} \)
17 \( 1 + (1.67 + 0.448i)T + (0.866 + 0.5i)T^{2} \)
19 \( 1 + (-0.866 + 0.5i)T^{2} \)
23 \( 1 + iT^{2} \)
29 \( 1 + (1.22 + 1.22i)T + iT^{2} \)
31 \( 1 + iT^{2} \)
41 \( 1 + (0.258 - 0.448i)T + (-0.5 - 0.866i)T^{2} \)
43 \( 1 - iT^{2} \)
47 \( 1 + T^{2} \)
53 \( 1 + (-1.22 + 0.707i)T + (0.5 - 0.866i)T^{2} \)
59 \( 1 + (-0.866 - 0.5i)T^{2} \)
61 \( 1 + (0.5 + 1.86i)T + (-0.866 + 0.5i)T^{2} \)
67 \( 1 + (-0.5 - 0.866i)T^{2} \)
71 \( 1 + (-0.5 - 0.866i)T^{2} \)
73 \( 1 - T^{2} \)
79 \( 1 + (-0.866 + 0.5i)T^{2} \)
83 \( 1 + (-0.5 + 0.866i)T^{2} \)
89 \( 1 + (0.258 - 0.965i)T + (-0.866 - 0.5i)T^{2} \)
97 \( 1 + (0.366 + 0.366i)T + iT^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

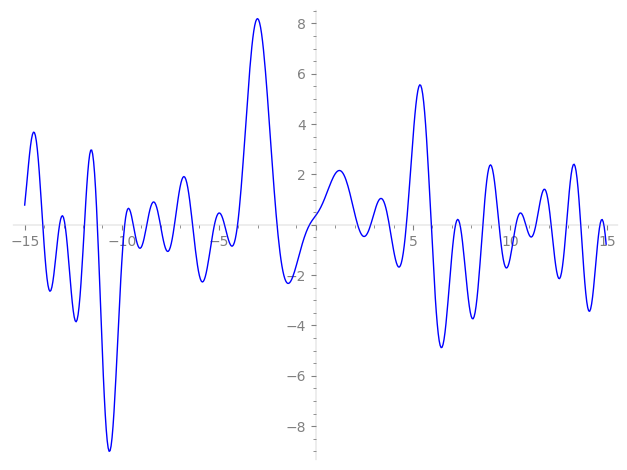
Imaginary part of the first few zeros on the critical line

−9.407150202018582992376092508503, −8.710462397117497720031738115122, −8.010002189661129383652961922912, −7.28528473319063735079488556948, −6.35254655164834961716952533002, −5.22615856690990462996530383655, −4.70605981670910318006786091409, −4.03557955053383243162936116963, −2.00121290385549564476465688502, −0.32884731423221698640502002362, 2.15025920554857763288385247919, 2.82085664481829600162904896979, 3.77895612041739039741648567862, 4.65987313192819089878180434369, 5.94090146894775108878910821304, 7.19263550311315262022211589683, 7.42176654464588595858812208694, 8.599221211509861176245769951979, 9.432606590090073249489692115928, 10.30244033008582094153941791751

Graph of the $Z$-function along the critical line