↑

Properties

Label 2-2160-240.203-c0-0-0
Degree $2$
Conductor $2160$
Sign $0.160 - 0.987i$
Analytic cond. $1.07798$
Root an. cond. $1.03825$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.707 + 0.707i)2-s − 1.00i·4-s + (−0.707 + 0.707i)5-s + (0.707 + 0.707i)8-s − 1.00i·10-s + (−0.707 − 0.707i)11-s + 13-s − 1.00·16-s + (0.707 + 0.707i)17-s + (0.707 + 0.707i)20-s + 1.00·22-s + (0.707 − 0.707i)23-s − 1.00i·25-s + (−0.707 + 0.707i)26-s + (−0.707 + 0.707i)29-s + ⋯
L(s)  = 1  + (−0.707 + 0.707i)2-s − 1.00i·4-s + (−0.707 + 0.707i)5-s + (0.707 + 0.707i)8-s − 1.00i·10-s + (−0.707 − 0.707i)11-s + 13-s − 1.00·16-s + (0.707 + 0.707i)17-s + (0.707 + 0.707i)20-s + 1.00·22-s + (0.707 − 0.707i)23-s − 1.00i·25-s + (−0.707 + 0.707i)26-s + (−0.707 + 0.707i)29-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2160 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.160 - 0.987i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2160 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.160 - 0.987i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2160\)    =    \(2^{4} \cdot 3^{3} \cdot 5\)
Sign: $0.160 - 0.987i$
Analytic conductor: \(1.07798\)
Root analytic conductor: \(1.03825\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2160} (1403, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2160,\ (\ :0),\ 0.160 - 0.987i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.7018935194\)
\(L(\frac12)\) \(\approx\) \(0.7018935194\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (0.707 - 0.707i)T \)
3 \( 1 \)
5 \( 1 + (0.707 - 0.707i)T \)
good7 \( 1 - iT^{2} \)
11 \( 1 + (0.707 + 0.707i)T + iT^{2} \)
13 \( 1 - T + T^{2} \)
17 \( 1 + (-0.707 - 0.707i)T + iT^{2} \)
19 \( 1 - iT^{2} \)
23 \( 1 + (-0.707 + 0.707i)T - iT^{2} \)
29 \( 1 + (0.707 - 0.707i)T - iT^{2} \)
31 \( 1 - iT - T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 - 1.41T + T^{2} \)
43 \( 1 - T + T^{2} \)
47 \( 1 + (0.707 - 0.707i)T - iT^{2} \)
53 \( 1 - 1.41T + T^{2} \)
59 \( 1 - iT^{2} \)
61 \( 1 + (1 - i)T - iT^{2} \)
67 \( 1 + 2T + T^{2} \)
71 \( 1 - T^{2} \)
73 \( 1 - iT^{2} \)
79 \( 1 - T + T^{2} \)
83 \( 1 - 1.41T + T^{2} \)
89 \( 1 - T^{2} \)
97 \( 1 + (-1 + i)T - iT^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

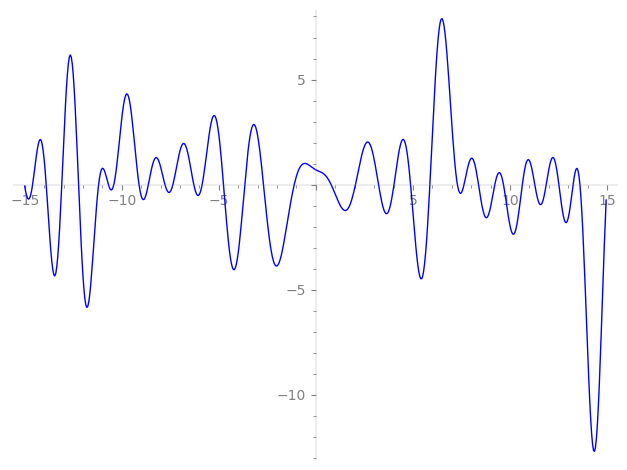
Imaginary part of the first few zeros on the critical line

−9.109101892281609351663237397370, −8.629834381163140730910205372796, −7.77432679554718394243505944495, −7.36610546865132212138019818895, −6.28804878744290457656649636560, −5.86014901763654521353025591785, −4.75940237151608450439752727147, −3.66466909963963894600455414189, −2.69936718627400046150890702690, −1.11715492894546494497931521665, 0.78519822039765553627000189864, 2.03708726662288201654305360948, 3.22721566942045914690209991482, 4.02217649545060334502972794743, 4.87647789558870307351524115810, 5.87005217889429243749792127137, 7.28861518056447071799652919132, 7.62929089082333278809450056496, 8.377059729341352950321407989913, 9.216113678600207724271230018648

Graph of the $Z$-function along the critical line