↑

Properties

Label 2-220-20.3-c1-0-15
Degree 22
Conductor 220220
Sign 0.764+0.644i0.764 + 0.644i
Analytic cond. 1.756701.75670
Root an. cond. 1.325401.32540
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.40 + 0.171i)2-s + (1.44 − 1.44i)3-s + (1.94 − 0.481i)4-s + (0.849 − 2.06i)5-s + (−1.77 + 2.27i)6-s + (3.60 + 3.60i)7-s + (−2.64 + 1.00i)8-s − 1.16i·9-s + (−0.837 + 3.04i)10-s − i·11-s + (2.10 − 3.49i)12-s + (−2.27 − 2.27i)13-s + (−5.67 − 4.44i)14-s + (−1.76 − 4.21i)15-s + (3.53 − 1.86i)16-s + (−3.21 + 3.21i)17-s + ⋯
L(s)  = 1  + (−0.992 + 0.121i)2-s + (0.833 − 0.833i)3-s + (0.970 − 0.240i)4-s + (0.379 − 0.925i)5-s + (−0.726 + 0.928i)6-s + (1.36 + 1.36i)7-s + (−0.934 + 0.356i)8-s − 0.388i·9-s + (−0.264 + 0.964i)10-s − 0.301i·11-s + (0.608 − 1.00i)12-s + (−0.630 − 0.630i)13-s + (−1.51 − 1.18i)14-s + (−0.454 − 1.08i)15-s + (0.884 − 0.467i)16-s + (−0.780 + 0.780i)17-s + ⋯

Functional equation

Λ(s)=(220s/2 ΓC(s) L(s)=((0.764+0.644i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 220 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.764 + 0.644i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(220s/2 ΓC(s+1/2) L(s)=((0.764+0.644i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 220 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.764 + 0.644i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 220220    =    22⋅5⋅112^{2} \cdot 5 \cdot 11
Sign: 0.764+0.644i0.764 + 0.644i
Analytic conductor: 1.756701.75670
Root analytic conductor: 1.325401.32540
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ220(23,⋅)\chi_{220} (23, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 220, ( :1/2), 0.764+0.644i)(2,\ 220,\ (\ :1/2),\ 0.764 + 0.644i)

Particular Values

L(1)L(1) ≈\approx 1.11131−0.405586i1.11131 - 0.405586i
L(12)L(\frac12) ≈\approx 1.11131−0.405586i1.11131 - 0.405586i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(1.40−0.171i)T 1 + (1.40 - 0.171i)T
5 1+(−0.849+2.06i)T 1 + (-0.849 + 2.06i)T
11 1+iT 1 + iT
good3 1+(−1.44+1.44i)T−3iT2 1 + (-1.44 + 1.44i)T - 3iT^{2}
7 1+(−3.60−3.60i)T+7iT2 1 + (-3.60 - 3.60i)T + 7iT^{2}
13 1+(2.27+2.27i)T+13iT2 1 + (2.27 + 2.27i)T + 13iT^{2}
17 1+(3.21−3.21i)T−17iT2 1 + (3.21 - 3.21i)T - 17iT^{2}
19 1−1.17T+19T2 1 - 1.17T + 19T^{2}
23 1+(1.72−1.72i)T−23iT2 1 + (1.72 - 1.72i)T - 23iT^{2}
29 1+8.70iT−29T2 1 + 8.70iT - 29T^{2}
31 1+2.23iT−31T2 1 + 2.23iT - 31T^{2}
37 1+(4.21−4.21i)T−37iT2 1 + (4.21 - 4.21i)T - 37iT^{2}
41 1+1.59T+41T2 1 + 1.59T + 41T^{2}
43 1+(4.09−4.09i)T−43iT2 1 + (4.09 - 4.09i)T - 43iT^{2}
47 1+(0.691+0.691i)T+47iT2 1 + (0.691 + 0.691i)T + 47iT^{2}
53 1+(3.07+3.07i)T+53iT2 1 + (3.07 + 3.07i)T + 53iT^{2}
59 1−3.06T+59T2 1 - 3.06T + 59T^{2}
61 1+3.44T+61T2 1 + 3.44T + 61T^{2}
67 1+(4.51+4.51i)T+67iT2 1 + (4.51 + 4.51i)T + 67iT^{2}
71 1−10.0iT−71T2 1 - 10.0iT - 71T^{2}
73 1+(−6.84−6.84i)T+73iT2 1 + (-6.84 - 6.84i)T + 73iT^{2}
79 1+0.973T+79T2 1 + 0.973T + 79T^{2}
83 1+(−0.453+0.453i)T−83iT2 1 + (-0.453 + 0.453i)T - 83iT^{2}
89 1−4.23iT−89T2 1 - 4.23iT - 89T^{2}
97 1+(−7.14+7.14i)T−97iT2 1 + (-7.14 + 7.14i)T - 97iT^{2}
show more
show less
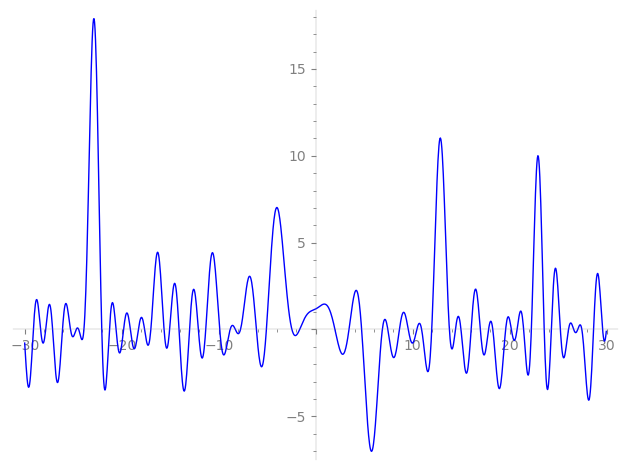
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.09750564678114081663752787049, −11.33730367539888552506620928178, −9.897425308822187993135215382115, −8.822850224362638479310476345185, −8.283423179890846360680478641926, −7.75583483743621505364820571061, −6.11667864919122207599991818756, −5.08569246358643107240420504906, −2.45350545364561619093950087858, −1.65613977053951714189558617124, 1.98255276241600182583495254897, 3.42911804521163661870955677299, 4.73177467559011348929950656704, 6.86753902431564649805475067607, 7.43376770045736862604293991387, 8.627904554195719399823574697970, 9.540972197050607005236152036261, 10.42340688957783436198945029180, 10.91690435608967953768111848301, 11.95789803317719244699753721010

Graph of the ZZ-function along the critical line