↑

Properties

Label 2-2600-2600.1091-c0-0-3
Degree $2$
Conductor $2600$
Sign $0.604 - 0.796i$
Analytic cond. $1.29756$
Root an. cond. $1.13910$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.809 + 0.587i)2-s + (−0.309 − 0.951i)3-s + (0.309 + 0.951i)4-s + (0.5 + 0.866i)5-s + (0.309 − 0.951i)6-s + 0.209·7-s + (−0.309 + 0.951i)8-s + (−0.104 + 0.994i)10-s + (0.809 − 0.587i)12-s + (0.809 − 0.587i)13-s + (0.169 + 0.122i)14-s + (0.669 − 0.743i)15-s + (−0.809 + 0.587i)16-s + (−0.604 + 1.86i)17-s + (−0.669 + 0.743i)20-s + (−0.0646 − 0.198i)21-s + ⋯
L(s)  = 1  + (0.809 + 0.587i)2-s + (−0.309 − 0.951i)3-s + (0.309 + 0.951i)4-s + (0.5 + 0.866i)5-s + (0.309 − 0.951i)6-s + 0.209·7-s + (−0.309 + 0.951i)8-s + (−0.104 + 0.994i)10-s + (0.809 − 0.587i)12-s + (0.809 − 0.587i)13-s + (0.169 + 0.122i)14-s + (0.669 − 0.743i)15-s + (−0.809 + 0.587i)16-s + (−0.604 + 1.86i)17-s + (−0.669 + 0.743i)20-s + (−0.0646 − 0.198i)21-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2600 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.604 - 0.796i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2600 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.604 - 0.796i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2600\)    =    \(2^{3} \cdot 5^{2} \cdot 13\)
Sign: $0.604 - 0.796i$
Analytic conductor: \(1.29756\)
Root analytic conductor: \(1.13910\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2600} (1091, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2600,\ (\ :0),\ 0.604 - 0.796i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.984545251\)
\(L(\frac12)\) \(\approx\) \(1.984545251\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.809 - 0.587i)T \)
5 \( 1 + (-0.5 - 0.866i)T \)
13 \( 1 + (-0.809 + 0.587i)T \)
good3 \( 1 + (0.309 + 0.951i)T + (-0.809 + 0.587i)T^{2} \)
7 \( 1 - 0.209T + T^{2} \)
11 \( 1 + (-0.309 - 0.951i)T^{2} \)
17 \( 1 + (0.604 - 1.86i)T + (-0.809 - 0.587i)T^{2} \)
19 \( 1 + (0.809 + 0.587i)T^{2} \)
23 \( 1 + (-0.309 - 0.951i)T^{2} \)
29 \( 1 + (0.809 - 0.587i)T^{2} \)
31 \( 1 + (-0.5 + 1.53i)T + (-0.809 - 0.587i)T^{2} \)
37 \( 1 + (-1.08 + 0.786i)T + (0.309 - 0.951i)T^{2} \)
41 \( 1 + (-0.309 + 0.951i)T^{2} \)
43 \( 1 + 0.209T + T^{2} \)
47 \( 1 + (-0.604 - 1.86i)T + (-0.809 + 0.587i)T^{2} \)
53 \( 1 + (0.809 - 0.587i)T^{2} \)
59 \( 1 + (-0.309 + 0.951i)T^{2} \)
61 \( 1 + (-0.309 - 0.951i)T^{2} \)
67 \( 1 + (0.809 + 0.587i)T^{2} \)
71 \( 1 + (0.413 + 1.27i)T + (-0.809 + 0.587i)T^{2} \)
73 \( 1 + (-0.309 - 0.951i)T^{2} \)
79 \( 1 + (0.809 - 0.587i)T^{2} \)
83 \( 1 + (0.809 + 0.587i)T^{2} \)
89 \( 1 + (-0.309 - 0.951i)T^{2} \)
97 \( 1 + (0.809 - 0.587i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

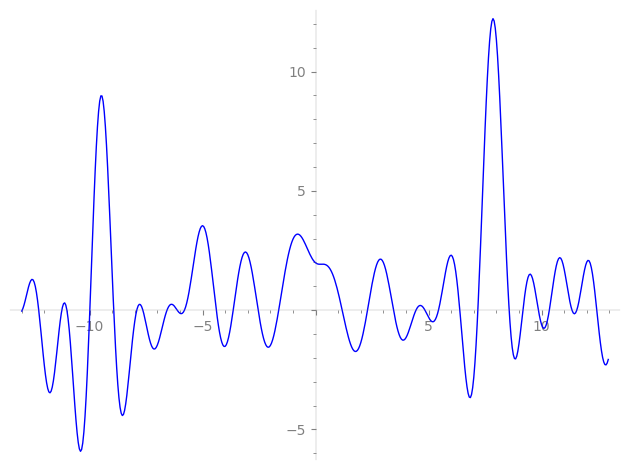
Imaginary part of the first few zeros on the critical line

−8.929552080209667701559174666628, −7.910457969348046967544524559556, −7.64112378812113378471144616109, −6.57254419971491815371155506973, −6.12157977110801661170824127245, −5.80087172539769623501617847675, −4.39058661911185907421266775820, −3.64421445832829662485371011364, −2.53899628218013657918421247473, −1.63052232284242745040285389947, 1.17700883407338429930810536752, 2.29781808674198310552429290001, 3.44810014062428063497923132788, 4.44318092725068435045112300417, 4.83796012087468033544371435806, 5.43768513778952520158699161131, 6.38184806224669868836192324349, 7.17975173253572534292645553431, 8.565995313950494648205671754897, 9.174977091239441954253273558647

Graph of the $Z$-function along the critical line