↑

Properties

Label 2-2695-2695.1044-c0-0-3
Degree $2$
Conductor $2695$
Sign $-0.462 - 0.886i$
Analytic cond. $1.34498$
Root an. cond. $1.15973$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

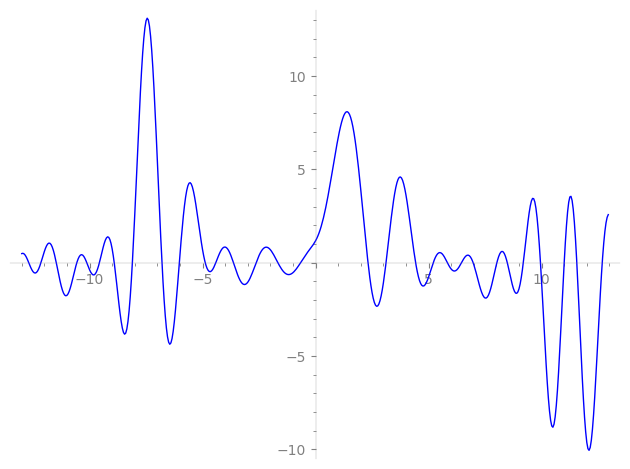
L(s)  = 1  + (0.400 − 1.75i)2-s + (−2.02 − 0.974i)4-s + (0.623 − 0.781i)5-s + (−0.222 − 0.974i)7-s + (−1.40 + 1.75i)8-s + (−0.222 − 0.974i)9-s + (−1.12 − 1.40i)10-s + (−0.222 + 0.974i)11-s + (0.0990 − 0.433i)13-s − 1.80·14-s + (1.12 + 1.40i)16-s + (−1.12 + 0.541i)17-s − 1.80·18-s + (−2.02 + 0.974i)20-s + (1.62 + 0.781i)22-s + ⋯
L(s)  = 1  + (0.400 − 1.75i)2-s + (−2.02 − 0.974i)4-s + (0.623 − 0.781i)5-s + (−0.222 − 0.974i)7-s + (−1.40 + 1.75i)8-s + (−0.222 − 0.974i)9-s + (−1.12 − 1.40i)10-s + (−0.222 + 0.974i)11-s + (0.0990 − 0.433i)13-s − 1.80·14-s + (1.12 + 1.40i)16-s + (−1.12 + 0.541i)17-s − 1.80·18-s + (−2.02 + 0.974i)20-s + (1.62 + 0.781i)22-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2695 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.462 - 0.886i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2695 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.462 - 0.886i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2695\)    =    \(5 \cdot 7^{2} \cdot 11\)
Sign: $-0.462 - 0.886i$
Analytic conductor: \(1.34498\)
Root analytic conductor: \(1.15973\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2695} (1044, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2695,\ (\ :0),\ -0.462 - 0.886i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.175276833\)
\(L(\frac12)\) \(\approx\) \(1.175276833\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad5 \( 1 + (-0.623 + 0.781i)T \)
7 \( 1 + (0.222 + 0.974i)T \)
11 \( 1 + (0.222 - 0.974i)T \)
good2 \( 1 + (-0.400 + 1.75i)T + (-0.900 - 0.433i)T^{2} \)
3 \( 1 + (0.222 + 0.974i)T^{2} \)
13 \( 1 + (-0.0990 + 0.433i)T + (-0.900 - 0.433i)T^{2} \)
17 \( 1 + (1.12 - 0.541i)T + (0.623 - 0.781i)T^{2} \)
19 \( 1 - T^{2} \)
23 \( 1 + (-0.623 - 0.781i)T^{2} \)
29 \( 1 + (-0.623 + 0.781i)T^{2} \)
31 \( 1 - 2T + T^{2} \)
37 \( 1 + (-0.623 + 0.781i)T^{2} \)
41 \( 1 + (0.222 + 0.974i)T^{2} \)
43 \( 1 + (0.277 + 0.347i)T + (-0.222 + 0.974i)T^{2} \)
47 \( 1 + (0.900 + 0.433i)T^{2} \)
53 \( 1 + (-0.623 - 0.781i)T^{2} \)
59 \( 1 + (0.277 + 0.347i)T + (-0.222 + 0.974i)T^{2} \)
61 \( 1 + (-0.623 + 0.781i)T^{2} \)
67 \( 1 - T^{2} \)
71 \( 1 + (-1.62 - 0.781i)T + (0.623 + 0.781i)T^{2} \)
73 \( 1 + (0.277 + 1.21i)T + (-0.900 + 0.433i)T^{2} \)
79 \( 1 - T^{2} \)
83 \( 1 + (0.445 + 1.94i)T + (-0.900 + 0.433i)T^{2} \)
89 \( 1 + (-0.0990 - 0.433i)T + (-0.900 + 0.433i)T^{2} \)
97 \( 1 - T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.907813485557227206725484982560, −8.105446911156888602132612842448, −6.79490691067171823247071494875, −6.02739009899954196266417031280, −4.88111949697985815194767182531, −4.41453483732496577930761410258, −3.63213090052810381425084531968, −2.63030301991671303054168064457, −1.66666898889664240597976311163, −0.66420208121727545364211250261, 2.32093845688993261484988632149, 3.11736329510512747983408362564, 4.42740974241054726342716054016, 5.20637601679095507984891318945, 5.83305309517963121809262169677, 6.45554149769377218489736544849, 6.97150096717538988770257263991, 8.020793456000352868939736123277, 8.482436954345827448653835620565, 9.190505982028224704526152455336

Graph of the $Z$-function along the critical line