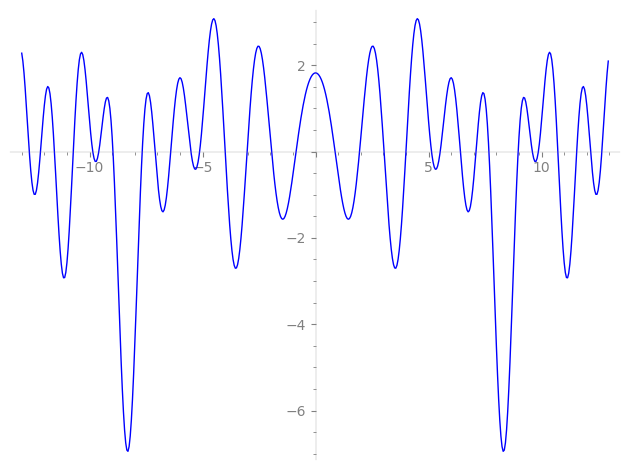
| L(s) = 1 | − 3-s + 2·5-s − 7-s + 9-s + 4·11-s − 6·13-s − 2·15-s + 6·17-s + 19-s + 21-s + 8·23-s − 25-s − 27-s − 6·29-s − 4·33-s − 2·35-s − 2·37-s + 6·39-s + 6·41-s − 4·43-s + 2·45-s + 4·47-s + 49-s − 6·51-s + 2·53-s + 8·55-s − 57-s + ⋯ |
| L(s) = 1 | − 0.577·3-s + 0.894·5-s − 0.377·7-s + 1/3·9-s + 1.20·11-s − 1.66·13-s − 0.516·15-s + 1.45·17-s + 0.229·19-s + 0.218·21-s + 1.66·23-s − 1/5·25-s − 0.192·27-s − 1.11·29-s − 0.696·33-s − 0.338·35-s − 0.328·37-s + 0.960·39-s + 0.937·41-s − 0.609·43-s + 0.298·45-s + 0.583·47-s + 1/7·49-s − 0.840·51-s + 0.274·53-s + 1.07·55-s − 0.132·57-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(1)\) |
\(\approx\) |
\(1.821773447\) |
| \(L(\frac12)\) |
\(\approx\) |
\(1.821773447\) |
| \(L(\frac{3}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 \) |
| 3 | \( 1 + T \) |
| 7 | \( 1 + T \) |
| 19 | \( 1 - T \) |
| good | 5 | \( 1 - 2 T + p T^{2} \) |
| 11 | \( 1 - 4 T + p T^{2} \) |
| 13 | \( 1 + 6 T + p T^{2} \) |
| 17 | \( 1 - 6 T + p T^{2} \) |
| 23 | \( 1 - 8 T + p T^{2} \) |
| 29 | \( 1 + 6 T + p T^{2} \) |
| 31 | \( 1 + p T^{2} \) |
| 37 | \( 1 + 2 T + p T^{2} \) |
| 41 | \( 1 - 6 T + p T^{2} \) |
| 43 | \( 1 + 4 T + p T^{2} \) |
| 47 | \( 1 - 4 T + p T^{2} \) |
| 53 | \( 1 - 2 T + p T^{2} \) |
| 59 | \( 1 - 12 T + p T^{2} \) |
| 61 | \( 1 + 10 T + p T^{2} \) |
| 67 | \( 1 - 8 T + p T^{2} \) |
| 71 | \( 1 + p T^{2} \) |
| 73 | \( 1 - 10 T + p T^{2} \) |
| 79 | \( 1 + 12 T + p T^{2} \) |
| 83 | \( 1 - 16 T + p T^{2} \) |
| 89 | \( 1 - 6 T + p T^{2} \) |
| 97 | \( 1 + 10 T + p T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
−8.963775622643969413086392004501, −7.66993740668373761303933835628, −7.09894490620541742508641698691, −6.40806092386379345620843510689, −5.51505027902262321429777131328, −5.13009745693058363129763091752, −3.99865329181363050042784951058, −3.02919764202190103672697538221, −1.94542814344019189651266846425, −0.861896809656660763138675843698,
0.861896809656660763138675843698, 1.94542814344019189651266846425, 3.02919764202190103672697538221, 3.99865329181363050042784951058, 5.13009745693058363129763091752, 5.51505027902262321429777131328, 6.40806092386379345620843510689, 7.09894490620541742508641698691, 7.66993740668373761303933835628, 8.963775622643969413086392004501