↑

Properties

Label 2-3192-3192.293-c0-0-4
Degree $2$
Conductor $3192$
Sign $0.0977 + 0.995i$
Analytic cond. $1.59301$
Root an. cond. $1.26214$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

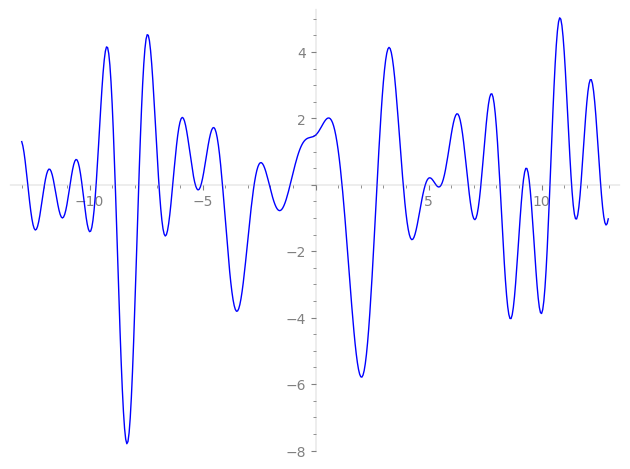
L(s)  = 1  + (0.5 − 0.866i)2-s + (−0.866 − 0.5i)3-s + (−0.499 − 0.866i)4-s + (0.866 + 0.5i)5-s + (−0.866 + 0.499i)6-s + 7-s − 0.999·8-s + (0.499 + 0.866i)9-s + (0.866 − 0.499i)10-s + 0.999i·12-s + (−0.866 + 0.5i)13-s + (0.5 − 0.866i)14-s + (−0.499 − 0.866i)15-s + (−0.5 + 0.866i)16-s + 0.999·18-s + (0.866 + 0.5i)19-s + ⋯
L(s)  = 1  + (0.5 − 0.866i)2-s + (−0.866 − 0.5i)3-s + (−0.499 − 0.866i)4-s + (0.866 + 0.5i)5-s + (−0.866 + 0.499i)6-s + 7-s − 0.999·8-s + (0.499 + 0.866i)9-s + (0.866 − 0.499i)10-s + 0.999i·12-s + (−0.866 + 0.5i)13-s + (0.5 − 0.866i)14-s + (−0.499 − 0.866i)15-s + (−0.5 + 0.866i)16-s + 0.999·18-s + (0.866 + 0.5i)19-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.0977 + 0.995i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.0977 + 0.995i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3192\)    =    \(2^{3} \cdot 3 \cdot 7 \cdot 19\)
Sign: $0.0977 + 0.995i$
Analytic conductor: \(1.59301\)
Root analytic conductor: \(1.26214\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3192} (293, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3192,\ (\ :0),\ 0.0977 + 0.995i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.496490422\)
\(L(\frac12)\) \(\approx\) \(1.496490422\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.5 + 0.866i)T \)
3 \( 1 + (0.866 + 0.5i)T \)
7 \( 1 - T \)
19 \( 1 + (-0.866 - 0.5i)T \)
good5 \( 1 + (-0.866 - 0.5i)T + (0.5 + 0.866i)T^{2} \)
11 \( 1 + T^{2} \)
13 \( 1 + (0.866 - 0.5i)T + (0.5 - 0.866i)T^{2} \)
17 \( 1 + (-0.5 - 0.866i)T^{2} \)
23 \( 1 + (-1.5 + 0.866i)T + (0.5 - 0.866i)T^{2} \)
29 \( 1 + (0.5 - 0.866i)T^{2} \)
31 \( 1 + T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 + (0.5 + 0.866i)T^{2} \)
43 \( 1 + (0.5 + 0.866i)T^{2} \)
47 \( 1 + (-0.5 + 0.866i)T^{2} \)
53 \( 1 + (0.5 - 0.866i)T^{2} \)
59 \( 1 + (-0.866 + 1.5i)T + (-0.5 - 0.866i)T^{2} \)
61 \( 1 + (-0.866 - 1.5i)T + (-0.5 + 0.866i)T^{2} \)
67 \( 1 + (-0.5 + 0.866i)T^{2} \)
71 \( 1 + (-0.5 + 0.866i)T + (-0.5 - 0.866i)T^{2} \)
73 \( 1 + (0.5 + 0.866i)T^{2} \)
79 \( 1 + (0.5 + 0.866i)T^{2} \)
83 \( 1 + iT - T^{2} \)
89 \( 1 + (0.5 - 0.866i)T^{2} \)
97 \( 1 + (-0.5 - 0.866i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.861498761055730257390243871084, −7.82322309861756655983741660636, −6.92797996854415093887789552043, −6.31956014410785507253996313075, −5.31833714962903270830358321995, −5.06688982887023827080769456020, −4.11897346773153145507215001079, −2.71865252490534595979859692798, −2.04451999782988839908146878045, −1.12487064132438352961850515991, 1.17107950347365331402196183306, 2.71815908182325246368245657223, 3.87886769325986953374021911015, 4.85401896802809214113491674251, 5.32542584834150263108818304527, 5.56143716035259711039699030330, 6.75518535107221849194960828199, 7.31487290995291755200036353332, 8.159561332948364338982196930529, 9.172393271590976973098316937339

Graph of the $Z$-function along the critical line