↑

Properties

Label 2-352-11.4-c1-0-8
Degree 22
Conductor 352352
Sign −0.751+0.659i-0.751 + 0.659i
Analytic cond. 2.810732.81073
Root an. cond. 1.676521.67652
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 11

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.5 + 1.53i)3-s + (−2.61 + 1.90i)5-s + (−1.38 − 4.25i)7-s + (0.309 + 0.224i)9-s + (−3.30 + 0.224i)11-s + (−1 − 0.726i)13-s + (−1.61 − 4.97i)15-s + (−1.5 + 1.08i)17-s + (1.66 − 5.11i)19-s + 7.23·21-s − 5.23·23-s + (1.69 − 5.20i)25-s + (−4.42 + 3.21i)27-s + (−2.61 − 8.05i)29-s + (0.381 + 0.277i)31-s + ⋯
L(s)  = 1  + (−0.288 + 0.888i)3-s + (−1.17 + 0.850i)5-s + (−0.522 − 1.60i)7-s + (0.103 + 0.0748i)9-s + (−0.997 + 0.0676i)11-s + (−0.277 − 0.201i)13-s + (−0.417 − 1.28i)15-s + (−0.363 + 0.264i)17-s + (0.381 − 1.17i)19-s + 1.57·21-s − 1.09·23-s + (0.338 − 1.04i)25-s + (−0.851 + 0.619i)27-s + (−0.486 − 1.49i)29-s + (0.0686 + 0.0498i)31-s + ⋯

Functional equation

Λ(s)=(352s/2 ΓC(s) L(s)=((−0.751+0.659i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 352 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.751 + 0.659i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(352s/2 ΓC(s+1/2) L(s)=((−0.751+0.659i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 352 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.751 + 0.659i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 352352    =    25⋅112^{5} \cdot 11
Sign: −0.751+0.659i-0.751 + 0.659i
Analytic conductor: 2.810732.81073
Root analytic conductor: 1.676521.67652
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ352(257,⋅)\chi_{352} (257, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 11
Selberg data: (2, 352, ( :1/2), −0.751+0.659i)(2,\ 352,\ (\ :1/2),\ -0.751 + 0.659i)

Particular Values

L(1)L(1) == 00
L(12)L(\frac12) == 00
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
11 1+(3.30−0.224i)T 1 + (3.30 - 0.224i)T
good3 1+(0.5−1.53i)T+(−2.42−1.76i)T2 1 + (0.5 - 1.53i)T + (-2.42 - 1.76i)T^{2}
5 1+(2.61−1.90i)T+(1.54−4.75i)T2 1 + (2.61 - 1.90i)T + (1.54 - 4.75i)T^{2}
7 1+(1.38+4.25i)T+(−5.66+4.11i)T2 1 + (1.38 + 4.25i)T + (-5.66 + 4.11i)T^{2}
13 1+(1+0.726i)T+(4.01+12.3i)T2 1 + (1 + 0.726i)T + (4.01 + 12.3i)T^{2}
17 1+(1.5−1.08i)T+(5.25−16.1i)T2 1 + (1.5 - 1.08i)T + (5.25 - 16.1i)T^{2}
19 1+(−1.66+5.11i)T+(−15.3−11.1i)T2 1 + (-1.66 + 5.11i)T + (-15.3 - 11.1i)T^{2}
23 1+5.23T+23T2 1 + 5.23T + 23T^{2}
29 1+(2.61+8.05i)T+(−23.4+17.0i)T2 1 + (2.61 + 8.05i)T + (-23.4 + 17.0i)T^{2}
31 1+(−0.381−0.277i)T+(9.57+29.4i)T2 1 + (-0.381 - 0.277i)T + (9.57 + 29.4i)T^{2}
37 1+(−2.85−8.78i)T+(−29.9+21.7i)T2 1 + (-2.85 - 8.78i)T + (-29.9 + 21.7i)T^{2}
41 1+(2.26−6.96i)T+(−33.1−24.0i)T2 1 + (2.26 - 6.96i)T + (-33.1 - 24.0i)T^{2}
43 1+4.09T+43T2 1 + 4.09T + 43T^{2}
47 1+(2−6.15i)T+(−38.0−27.6i)T2 1 + (2 - 6.15i)T + (-38.0 - 27.6i)T^{2}
53 1+(5.23+3.80i)T+(16.3+50.4i)T2 1 + (5.23 + 3.80i)T + (16.3 + 50.4i)T^{2}
59 1+(−2.80−8.64i)T+(−47.7+34.6i)T2 1 + (-2.80 - 8.64i)T + (-47.7 + 34.6i)T^{2}
61 1+(2−1.45i)T+(18.8−58.0i)T2 1 + (2 - 1.45i)T + (18.8 - 58.0i)T^{2}
67 1−1.38T+67T2 1 - 1.38T + 67T^{2}
71 1+(−3+2.17i)T+(21.9−67.5i)T2 1 + (-3 + 2.17i)T + (21.9 - 67.5i)T^{2}
73 1+(1.26+3.88i)T+(−59.0+42.9i)T2 1 + (1.26 + 3.88i)T + (-59.0 + 42.9i)T^{2}
79 1+(4.85+3.52i)T+(24.4+75.1i)T2 1 + (4.85 + 3.52i)T + (24.4 + 75.1i)T^{2}
83 1+(1.92−1.40i)T+(25.6−78.9i)T2 1 + (1.92 - 1.40i)T + (25.6 - 78.9i)T^{2}
89 1−6.38T+89T2 1 - 6.38T + 89T^{2}
97 1+(4.54+3.30i)T+(29.9+92.2i)T2 1 + (4.54 + 3.30i)T + (29.9 + 92.2i)T^{2}
show more
show less
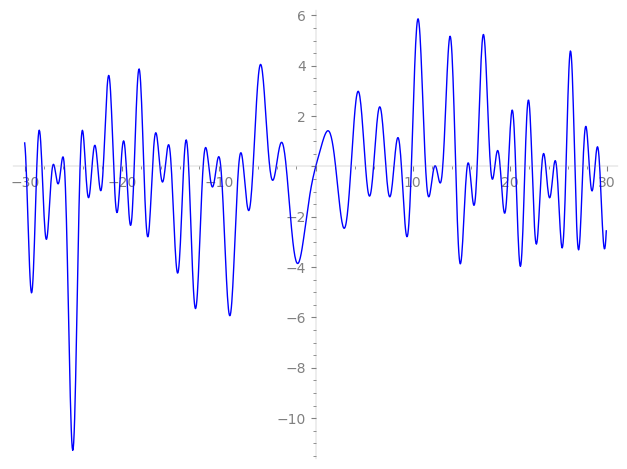
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.02057187369932880474590405706, −10.23437906467793589238101379297, −9.790307239538750785277506975410, −7.946437598492409176256447020654, −7.46098195988438707761063349612, −6.45311900967382577253584636680, −4.74593644084615635962368525140, −4.06661752714080717231614769577, −3.04719940887095986562796251707, 0, 2.04981031053179698684337632579, 3.64199558518092546762566709298, 5.13256061666897703691362413305, 5.96127071999746570565225057537, 7.22494039507714965586468935351, 8.066893630161135541193811681531, 8.833391827813415079616245940941, 9.860766434134297041671188187853, 11.31890009626581160904711270912

Graph of the ZZ-function along the critical line