↑

Properties

Label 2-370-185.8-c1-0-18
Degree 22
Conductor 370370
Sign −0.788+0.615i-0.788 + 0.615i
Analytic cond. 2.954462.95446
Root an. cond. 1.718851.71885
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.866 − 0.5i)2-s + (−0.765 − 2.85i)3-s + (0.499 − 0.866i)4-s + (2.10 − 0.751i)5-s + (−2.09 − 2.09i)6-s + (−0.920 − 3.43i)7-s − 0.999i·8-s + (−4.98 + 2.87i)9-s + (1.44 − 1.70i)10-s + 4.83i·11-s + (−2.85 − 0.765i)12-s + (3.57 + 2.06i)13-s + (−2.51 − 2.51i)14-s + (−3.76 − 5.44i)15-s + (−0.5 − 0.866i)16-s + (3.48 + 6.03i)17-s + ⋯
L(s)  = 1  + (0.612 − 0.353i)2-s + (−0.442 − 1.65i)3-s + (0.249 − 0.433i)4-s + (0.941 − 0.336i)5-s + (−0.854 − 0.854i)6-s + (−0.348 − 1.29i)7-s − 0.353i·8-s + (−1.66 + 0.959i)9-s + (0.457 − 0.538i)10-s + 1.45i·11-s + (−0.825 − 0.221i)12-s + (0.991 + 0.572i)13-s + (−0.672 − 0.672i)14-s + (−0.971 − 1.40i)15-s + (−0.125 − 0.216i)16-s + (0.845 + 1.46i)17-s + ⋯

Functional equation

Λ(s)=(370s/2 ΓC(s) L(s)=((−0.788+0.615i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 370 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.788 + 0.615i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(370s/2 ΓC(s+1/2) L(s)=((−0.788+0.615i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 370 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.788 + 0.615i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 370370    =    2⋅5⋅372 \cdot 5 \cdot 37
Sign: −0.788+0.615i-0.788 + 0.615i
Analytic conductor: 2.954462.95446
Root analytic conductor: 1.718851.71885
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ370(193,⋅)\chi_{370} (193, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 370, ( :1/2), −0.788+0.615i)(2,\ 370,\ (\ :1/2),\ -0.788 + 0.615i)

Particular Values

L(1)L(1) ≈\approx 0.593530−1.72506i0.593530 - 1.72506i
L(12)L(\frac12) ≈\approx 0.593530−1.72506i0.593530 - 1.72506i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−0.866+0.5i)T 1 + (-0.866 + 0.5i)T
5 1+(−2.10+0.751i)T 1 + (-2.10 + 0.751i)T
37 1+(3.80+4.74i)T 1 + (3.80 + 4.74i)T
good3 1+(0.765+2.85i)T+(−2.59+1.5i)T2 1 + (0.765 + 2.85i)T + (-2.59 + 1.5i)T^{2}
7 1+(0.920+3.43i)T+(−6.06+3.5i)T2 1 + (0.920 + 3.43i)T + (-6.06 + 3.5i)T^{2}
11 1−4.83iT−11T2 1 - 4.83iT - 11T^{2}
13 1+(−3.57−2.06i)T+(6.5+11.2i)T2 1 + (-3.57 - 2.06i)T + (6.5 + 11.2i)T^{2}
17 1+(−3.48−6.03i)T+(−8.5+14.7i)T2 1 + (-3.48 - 6.03i)T + (-8.5 + 14.7i)T^{2}
19 1+(1.30+4.86i)T+(−16.4+9.5i)T2 1 + (1.30 + 4.86i)T + (-16.4 + 9.5i)T^{2}
23 1−1.47iT−23T2 1 - 1.47iT - 23T^{2}
29 1+(2.37+2.37i)T+29iT2 1 + (2.37 + 2.37i)T + 29iT^{2}
31 1+(2.94−2.94i)T−31iT2 1 + (2.94 - 2.94i)T - 31iT^{2}
41 1+(−1.84−1.06i)T+(20.5+35.5i)T2 1 + (-1.84 - 1.06i)T + (20.5 + 35.5i)T^{2}
43 1−0.602iT−43T2 1 - 0.602iT - 43T^{2}
47 1+(2.33−2.33i)T−47iT2 1 + (2.33 - 2.33i)T - 47iT^{2}
53 1+(−0.651+2.42i)T+(−45.8−26.5i)T2 1 + (-0.651 + 2.42i)T + (-45.8 - 26.5i)T^{2}
59 1+(2.34+0.628i)T+(51.0+29.5i)T2 1 + (2.34 + 0.628i)T + (51.0 + 29.5i)T^{2}
61 1+(−1.69−6.31i)T+(−52.8+30.5i)T2 1 + (-1.69 - 6.31i)T + (-52.8 + 30.5i)T^{2}
67 1+(−8.93+2.39i)T+(58.0−33.5i)T2 1 + (-8.93 + 2.39i)T + (58.0 - 33.5i)T^{2}
71 1+(−5.05+8.75i)T+(−35.5−61.4i)T2 1 + (-5.05 + 8.75i)T + (-35.5 - 61.4i)T^{2}
73 1+(−9.08+9.08i)T−73iT2 1 + (-9.08 + 9.08i)T - 73iT^{2}
79 1+(−3.81−14.2i)T+(−68.4+39.5i)T2 1 + (-3.81 - 14.2i)T + (-68.4 + 39.5i)T^{2}
83 1+(−0.985+3.67i)T+(−71.8−41.5i)T2 1 + (-0.985 + 3.67i)T + (-71.8 - 41.5i)T^{2}
89 1+(2.51−9.39i)T+(−77.0−44.5i)T2 1 + (2.51 - 9.39i)T + (-77.0 - 44.5i)T^{2}
97 1+11.5T+97T2 1 + 11.5T + 97T^{2}
show more
show less
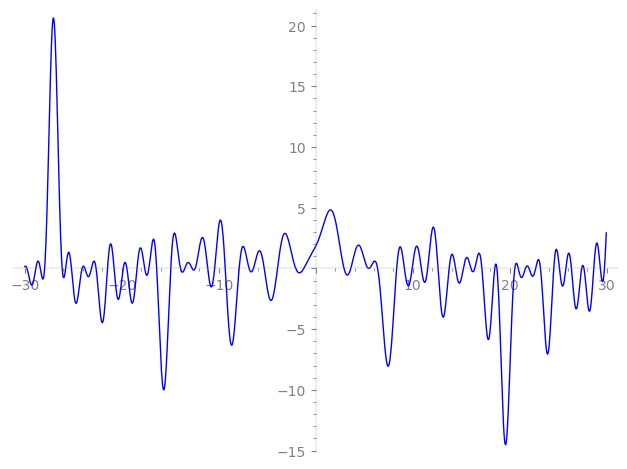
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.13502775576033663236058918347, −10.42092829643416969017767119443, −9.327679102608971268736306274759, −7.893081366737605768174969396837, −6.86822549190301812912144187460, −6.42263997352976296918562582306, −5.30649742789441783191507983645, −3.93902990012615312952132765417, −2.06043857745506889910521755065, −1.22789868162629254617862376201, 2.91599412954172665587942566527, 3.61727591713861369100154190083, 5.43336792908798295379962651226, 5.50666557687624731501860044018, 6.37814193634157440757872112580, 8.345449284173630527379532219998, 9.140239571423139242254985154577, 9.942526005968185908007231000781, 10.88794422852072864334394835360, 11.54153144131401361880182544190

Graph of the ZZ-function along the critical line